After the excitement of my previous post on the cause of relativistic length contraction, let me pause for a moment to discuss my revolutionary discovery with a hypothetical reader.
Reader: OK then, here's what I think: your supposed "revolutionary discovery" is quite redundant. Elementary textbooks make it clear that length contraction is a consequence of the relativity of simultaneity. For example, Leo Sartori (1996) states that length contraction "can be linked to the relativity of simultaneity" (p. 83). As he explains, "if ground observers measure the position of the front and rear ends of a moving train simultaneously according to their clocks, these measurements take place at different times according to train clocks. According to train observers, therefore, the length measured by ground observers is incorrect." No further explanation is required.
Me: With all due respect, any textbooks that interpret length contraction as a consequence of the "relativity of simultaneity" are mistaken. To see this, it is important to remember that the "relativity of simultaneity" is a result of the decision to use Einstein's clock adjustment procedure to adjust clocks in all inertial frames of reference. It would be equally possible to adjust clocks in a manner which makes "simultaneity" absolute, for example by using Einstein's clock adjustment procedure in just one inertial frame of reference and adjusting all other clocks to zero when they pass a clock in that frame showing zero. There would then be no "relativity of simultaneity". But all moving objects in the frame of reference in which clocks have been Einstein-adjusted would still be length-contracted. Which proves my point.
The truth is that length contraction in all inertial frames of reference in which clocks have been Einstein-adjusted is a fundamental empirical fact for which special relativity has no explanation. Unless the constancy of the two-way speed of light is accepted as a fundamental empirical fact, in which case length contraction follows. But that makes no sense because speed is derived from length and time measurements and therefore length contraction and time dilation are more fundamental than the constancy of the two-way speed of light.
Reader: I see that you enjoy picking holes in other people's arguments. Let me pick one in yours. You base your explanation of length contraction on the concept of force. There's a problem with that because the definition of force via Newton's laws of mechanics involves the concept of mass and requires the existence of time coordinates in any frame of reference in which forces are said to act. In your derivation of length contraction, however, you have not specified a clock adjustment procedure in the moving frame of reference, so you have not defined any time coordinates in that frame, let alone explained the concept of mass. Therefore, your reference to a force acting between two moving charges simply makes no sense.
Me: Point taken, I should have said a bit more about the concept of force underlying my previous post. What I had in mind was not so much Newton's laws but a static concept of force, in which, for example, a particular "force" is said to act on a spring if the spring is extended by a particular amount. Two such springs that are stationary in a frame of reference Σ in which light propagates in symmetrical conditions and clocks have been Einstein-adjusted can then be used to find experimentally that two charges exert forces on each other which are proportional to the amount of charge attached to either spring and inversely proportional to the square of the distance between the charges. This is nothing but the Coulomb law for stationary charges.
The same kind of experiments can be performed in any spatial inertial frame of reference S that moves relative to Σ, and the Coulomb law will be found to be valid in that frame, too. All of that can be done without defining any time coordinates in the moving frame and without defining mass. But these experimental findings do not tell us anything about length contraction. Indeed, they are compatible with any length contraction factor. And this is where my sphere model comes in.
Using this model, the Coulomb law can be formulated so that forces between charges that are stationary in S can be expressed as a function of their distance as measured in Σ. It would be found experimentally that this version of the Coulomb law predicts the correct force between such charges as measured in S using springs. This formulation of the Coulomb law can then be used to derive the length contraction factor in Σ in the manner shown in my previous post.
Reader: Even if you can resolve the force issue by relying on a very limited concept of force, it remains that your model is pretty tautological. It merely "explains" electric length contraction because you have adapted it to that purpose. You manipulate the Coulomb law in exactly such a way that you get the desired result. I'm sorry, but all of this does not add up to much of an explanation at all.
Me: Your objection is not unfounded but I suspect it could be applied to any model of the physical world. For we surely strive to design any such model in a manner which makes it correspond to what we find empirically. The real question, it seems to me, is whether we can get a model to explain a very broad range of phenomena while keeping it simple and plausible. In the case of the sphere model of electricity, initially I developed it not in order to explain length contraction but simply to explain the independence of the speed of light from its source. If anything, I came up with the sphere model despite the fact that at first sight it seemed quite incapable of explaining length contraction. It thus came as a surprise to me to find that length contraction can be explained quite naturally in terms of that model. The independence of the speed of light from its source and length contraction may not add up to a very broad range of phenomena, but I feel I've made a promising start! At the same time, I feel my model is reasonably plausible and astonishingly simple.
It is true that the plausibility or simplicity of any particular physical model is to some extent a matter of opinion. As Kevin Brown suggests in his Reflections on Relativity (2010),most physicists appear to accept a four-dimensional Minkowskian spacetime incorporating length contraction and time dilation as a sufficiently simple and plausible basic model that does not require any further explanation (p. 48). Fair enough. To me, however, length contraction and time dilation by the relativistic factor call for an explanation, more specifically an explanation that must somehow turn on how force field disturbances propagate. And that's what I'm trying to find, if only to satisfy my own curiosity.
Reader: That may be so, and good luck with it, but it seems to me that you are miles away from your goal since your explanation at best only explains "electric length contraction" and not "length contraction of everything".
Me: Absolutely, this is just a first step. But the very fact that everything is length-contracted by the relativistic factor suggests to me that the speed of light is also the speed at which any other field disturbances propagate, and that an explanation of electric length contraction can potentially serve as a template for an explanation of length contraction more generally. It also suggests to me that there is a fundamental unity to the physical world without which the world could not in fact function in the way it does.
Reader: You admit, then, that at the moment you can only - at best - explain "electric length contraction". Well, if that's all then it's no more than what Hendrik Lorentz did more than 100 years ago. Today this kind of "electric" length contraction, in other words the contraction of electric fields by the relativistic factor, is derived from Maxwell's equations in any textbook on classical electromagnetism. Once again, your "revolutionary" model, if it has any explanatory power at all, adds nothing to what has been known for over a century.
Me: Yes and no. Let me refer you back to my criteria for what makes for a good physical model: its applicability to a wide range of phenomena, its plausibility, and its simplicity. I'd suggest that the way electric length contraction is derived in classical electromagnetism falls foul of the third requirement: simplicity. Indeed, so long and complex is the chain of reasoning - involving the development of far-from-simple concepts such as electric and magnetic fields, a series of assumptions in the development of Maxwell's equations, and a range of advanced mathematical techniques - that in the end it is totally unclear what the explanation for electric length contraction really is. Indeed, I harbour a suspicion that length contraction and time dilation - or equivalently the constancy of the two-way speed of light - are somehow built into the premises of classical electromagnetism without explicitly acknowledging it.
Especially the "magnetic field" seems suspect to me. The basic equations of magnetism involve essentially the electric field constant and the speed of light, so magnetism seems to be no more than an electric phenomenon that comes about as a result of the fact that electric field disturbances in Σ propagate at c.
Clarifying all this would require a detailed examination of the logical structure of classical electromagnetism. As Kevin Brown's book Reflections on Relativity shows, fully understanding and, potentially, reformulating classical electromagnetism has occupied the minds of many illustrious physicists over the decades, so this will be no easy task. In truth, every time I leaf through that book I am reminded of this: if understanding physics, let alone the physical world, is to climb a mountain, then all I have achieved in this blog so far is to step on a molehill.
This blog is motivated by my desire to understand the special theory of relativity, in particular the principle of the constancy of the speed of light for every observer. How did physicists come to accept it? Is it based on convention, theory or observation? Are there any alternative conventions or theories that are compatible with observation and experiment?
Sunday, 17 March 2013
Sunday, 3 March 2013
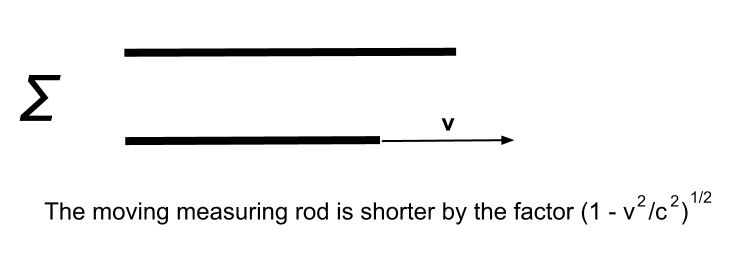
The cause of length contraction
The relativistic length contraction and time dilation factors in an inertial frame of reference Σ in which light propagates in symmetrical conditions in all directions and clocks have been synchronized using Einstein's method are of a very simple mathematical form and involve only two parameters: the speed v at which a body or clock travels in Σ and the speed c at which electric field disturbances, and perhaps any force field disturbances, travel in Σ.
This suggests that it should be possible to deduce length contraction and time dilation in Σ - and therefore the constancy of the two-way speed of light in any spatial inertial frame of reference - from a simple model of how field disturbances propagate in force fields.
In this post, I would like to make a start by attempting to deduce "electric length contraction" from a really simple model of electricity. In other words, I would like to show that all charged particles that are in a state of equilibrium in a measuring rod that is stationary in Σ will be in the same state of equilibrium in the same measuring rod moving at v through Σ if and only if the distances between them in the direction of movement are reduced by the relativistic factor. Is my sphere model of electricity up to the task?
Let me recall the basic idea behind the sphere model: the field around any charge that is stationary in Σ is represented as a series of concentric spheres with a particular sphere density λΣ:

When the charge is locally accelerated to a speed v in Σ and then continues to move at that speed, the information about the acceleration spreads through the spheres at the speed c, leading to the following situation after a time t has passed:
The basic sphere model law is that any electric field disturbance always traverses the same number of spheres in the same amount of time, as measured in Σ.
In this diagram, therefore, P1P2 = vt and P1P3 = ct. If the angle between P2P3 and v is α, the cosine rule can be applied to the triangle P1P2P3 to calculate P2P3, and that can in turn be used to determine the sphere density λα on P2P3 as a function of λΣ, v, c and α:

(Equation 1)
Let me now consider the Coulomb law for charges q1 and q2 which are stationary in Σ and separated by the distance r.

(Equation 2)
In the sphere model, what matters is not so much the distance r as such but, for a given sphere density λΣ, the number n1 of sphere surfaces around q1 cutting through r on the one hand, and the number n2 of sphere surfaces around q2 cutting through r on the other:
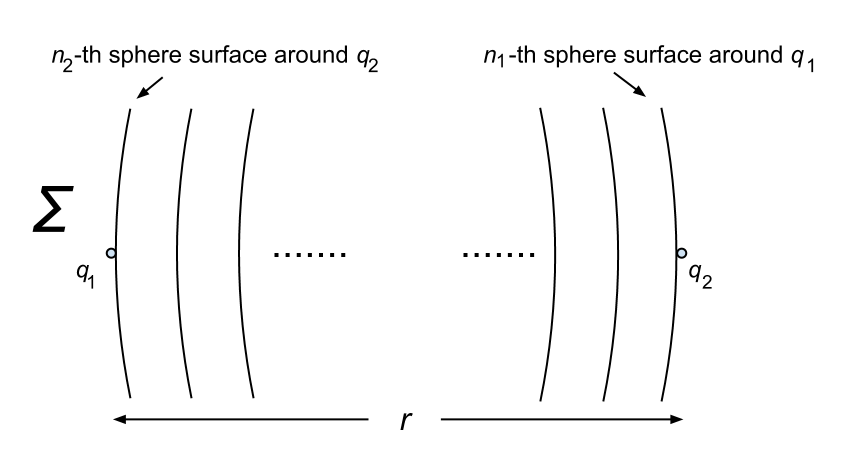
This is because what acts at q2 is the n1-th sphere surface around q1, and what acts at q1 is the n2-th sphere surface around q2.
For symmetry reasons, n2 = n1 , so we have:
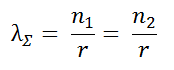
or
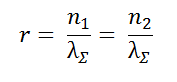
Inserting this into Equation 2, the Coulomb law can be rewritten as follows:
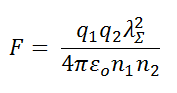
(Equation 3)
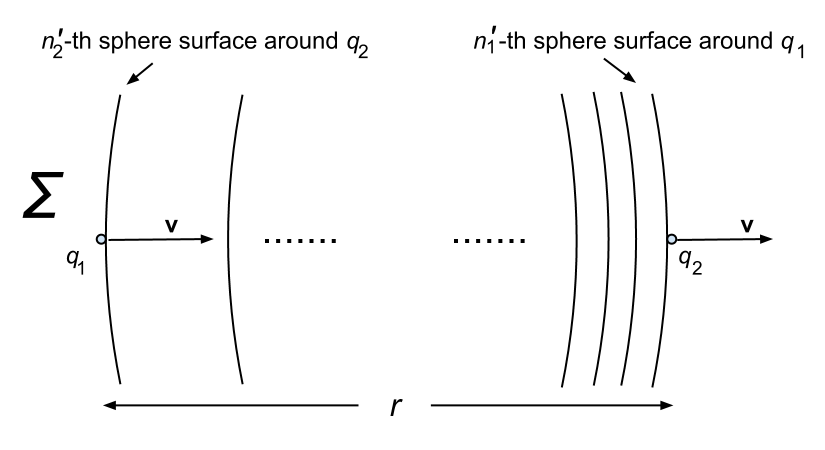
Now suppose the two charges have been accelerated to a speed v in Σ and are still separated by the distance r as measured in Σ.
The number of sphere surfaces surrounding q1 and cutting through r is then increased to n1', and the number of sphere surfaces surrounding q2 and cutting through r is reduced to n2', as shown below:
Using Equation 1, we obtain for the sphere densities λα=0 on the leading side of q1 and λα=π on the trailing side of q2:
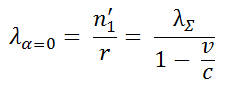
and
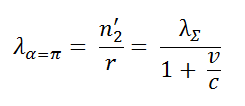
[PS: As indicated here, a more general analysis shows that the two densities that need to be considered are the density of q1 spheres over r (a) along the line connecting the two charges on the side facing towards q2 and (b) along the line connecting the two charges on the side facing away from q2 . The result in the case of two charges moving at the same velocity is the same, but in more general situations this is the approach that must be taken.]
Inserting n1' and n2' into (Equation 3) to replace n1 and n2, we thus obtain for the force between the two charges
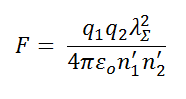
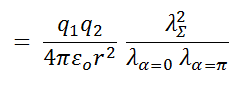
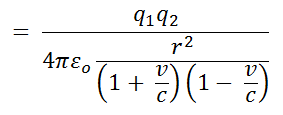

(Equation 4)
It turns out that this modified Coulomb law for a pair of moving charges even holds for any pair of sphere densities λα and λα+π , in other words it holds for any angle α between the connecting line between the two charges and v. However, if π>α >0 , then F in the direction that is perpendicular to v is further modified by magnetic effects, and I have not yet incorporated such effects into my model.
Limiting myself therefore to the case of α=0, Equation 4 shows that the electric force between q1 and q2 moving at v through Σ and separated by r is the same as the electric force between two charges q1 and q2 that are stationary in Σ and separated by r(1 - v2/c2)-1/2.
Conversely then, if the stationary charges q1 and q2 are separated by r in Σ and are then both accelerated to v, if the force between the moving q1 and q2 is to be the same as it was between the stationary q1 and q2, then the distance between them in terms of Σ coordinates must be reduced to:
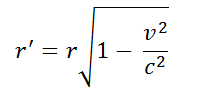
And this is the essence of "electric length contraction": all the charged particles that are in a state of equilibrium in a measuring rod that is stationary in Σ will be in the same state of equilibrium in the same measuring rod moving at v through Σ if and only if the distances between them in the direction of movement are reduced by the factor (1 - v2/c2)1/2.
What I have shown is that the "electric length contraction" of moving bodies by the relativistic factor as seen from an inertial frame of reference in which light propagates in symmetrical conditions in all directions and clocks are Einstein-adjusted is a natural consequence of my really simple sphere model of electricity.
I regard this as a major result, at least on a par with my earlier findings concerning "simultaneity" and "one-way speed" in special relativity.
Am I deluded? I will discuss that question in my next post.
This suggests that it should be possible to deduce length contraction and time dilation in Σ - and therefore the constancy of the two-way speed of light in any spatial inertial frame of reference - from a simple model of how field disturbances propagate in force fields.
In this post, I would like to make a start by attempting to deduce "electric length contraction" from a really simple model of electricity. In other words, I would like to show that all charged particles that are in a state of equilibrium in a measuring rod that is stationary in Σ will be in the same state of equilibrium in the same measuring rod moving at v through Σ if and only if the distances between them in the direction of movement are reduced by the relativistic factor. Is my sphere model of electricity up to the task?
Let me recall the basic idea behind the sphere model: the field around any charge that is stationary in Σ is represented as a series of concentric spheres with a particular sphere density λΣ:
When the charge is locally accelerated to a speed v in Σ and then continues to move at that speed, the information about the acceleration spreads through the spheres at the speed c, leading to the following situation after a time t has passed:
The basic sphere model law is that any electric field disturbance always traverses the same number of spheres in the same amount of time, as measured in Σ.
In this diagram, therefore, P1P2 = vt and P1P3 = ct. If the angle between P2P3 and v is α, the cosine rule can be applied to the triangle P1P2P3 to calculate P2P3, and that can in turn be used to determine the sphere density λα on P2P3 as a function of λΣ, v, c and α:
(Equation 1)
Let me now consider the Coulomb law for charges q1 and q2 which are stationary in Σ and separated by the distance r.
(Equation 2)
In the sphere model, what matters is not so much the distance r as such but, for a given sphere density λΣ, the number n1 of sphere surfaces around q1 cutting through r on the one hand, and the number n2 of sphere surfaces around q2 cutting through r on the other:
This is because what acts at q2 is the n1-th sphere surface around q1, and what acts at q1 is the n2-th sphere surface around q2.
For symmetry reasons, n2 = n1 , so we have:
or
Inserting this into Equation 2, the Coulomb law can be rewritten as follows:
(Equation 3)
Now suppose the two charges have been accelerated to a speed v in Σ and are still separated by the distance r as measured in Σ.
The number of sphere surfaces surrounding q1 and cutting through r is then increased to n1', and the number of sphere surfaces surrounding q2 and cutting through r is reduced to n2', as shown below:
Using Equation 1, we obtain for the sphere densities λα=0 on the leading side of q1 and λα=π on the trailing side of q2:
and
[PS: As indicated here, a more general analysis shows that the two densities that need to be considered are the density of q1 spheres over r (a) along the line connecting the two charges on the side facing towards q2 and (b) along the line connecting the two charges on the side facing away from q2 . The result in the case of two charges moving at the same velocity is the same, but in more general situations this is the approach that must be taken.]
Inserting n1' and n2' into (Equation 3) to replace n1 and n2, we thus obtain for the force between the two charges
(Equation 4)
It turns out that this modified Coulomb law for a pair of moving charges even holds for any pair of sphere densities λα and λα+π , in other words it holds for any angle α between the connecting line between the two charges and v. However, if π>α >0 , then F in the direction that is perpendicular to v is further modified by magnetic effects, and I have not yet incorporated such effects into my model.
Limiting myself therefore to the case of α=0, Equation 4 shows that the electric force between q1 and q2 moving at v through Σ and separated by r is the same as the electric force between two charges q1 and q2 that are stationary in Σ and separated by r(1 - v2/c2)-1/2.
Conversely then, if the stationary charges q1 and q2 are separated by r in Σ and are then both accelerated to v, if the force between the moving q1 and q2 is to be the same as it was between the stationary q1 and q2, then the distance between them in terms of Σ coordinates must be reduced to:
And this is the essence of "electric length contraction": all the charged particles that are in a state of equilibrium in a measuring rod that is stationary in Σ will be in the same state of equilibrium in the same measuring rod moving at v through Σ if and only if the distances between them in the direction of movement are reduced by the factor (1 - v2/c2)1/2.
What I have shown is that the "electric length contraction" of moving bodies by the relativistic factor as seen from an inertial frame of reference in which light propagates in symmetrical conditions in all directions and clocks are Einstein-adjusted is a natural consequence of my really simple sphere model of electricity.
I regard this as a major result, at least on a par with my earlier findings concerning "simultaneity" and "one-way speed" in special relativity.
Am I deluded? I will discuss that question in my next post.
Subscribe to:
Posts (Atom)