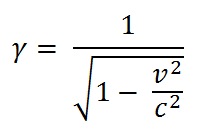One of the few attempts to justify Einstein's clock adjustment procedure that I have seen in the literature is contained in a book by Max Born, Einstein's Theory of Relativity, first published in German in 1920. New editions were published in English in 1962 and in German in 1964.
In the 1964 edition, Born describes a clock adjustment procedure which is essentially equivalent to that presented by Einstein in his 1905 article: clocks in A and B in a uniformly moving frame of reference are adjusted to show the same time when a flash of light emanating from the midpoint C of a straight line between A and B reaches the clocks. Born notes that, if sound signals rather than light signals are used, this procedure results in disagreements between different frames of reference over which events are simultaneous. He adds that, in the case of sound, only the frame of reference that is at rest relative to the body of air in which the sound propagates has the right time, but no such distinction can be made if light signals are used 'because absolute movement relative to the light ether is a concept which, according to all our experience, has no physical reality'.
Born concludes that the procedure can be applied in any frame of reference using light signals. But since light signals observe the same no-overtaking rule as sound signals, the same kinds of disagreement arise, in other words 'if two such frames moving uniformly and in a straight line relative to each other meet and, for example, the clocks A and A' show the same time, then the hands of clocks B and B' will be in different positions. Both frames are equally entitled to claim that they have the right time, for each can maintain that it is at rest because all laws of nature are the same in both frames. But if two are equally entitled to make the same claim, which by its very nature can only be granted to one, then we must conclude that the claim is in fact meaningless: There is no absolute simultaneity. Once this has been grasped, it is difficult to understand that many centuries of exact research had to pass before this simple fact was recognized.' (pp. 197-98)
Born is right to say that, if a light ether existed, Einstein's clock adjustment procedure would not constitute a synchronization procedure in all frames of reference. However, the absence of an ether does not mean that Einstein's clock adjustment constitutes a synchronization procedure. This is because the real test for the usability of Einstein's clock adjustment procedure as a synchronization procedure is not whether or not there is a universal medium in which the signals propagate but, much more generally, whether or not the conditions in which the signals are emitted or propagate are symmetrical in opposite directions.
Whatever those signals are - waves in a universal medium; particles that are ejected without the need for a medium; or something else - it is clear that if the conditions of emission and propagation are symmetrical in opposite directions in one frame of reference, then they cannot also be symmetrical for the very same signals from the point of view of an observer who is moving relative to that frame of reference.
It is true that, if we don't know whether those conditions are symmetrical in two given frames of reference, then those two frames are equally entitled, or rather equally ill-placed, to claim that they have the right time if their clocks are Einstein-adjusted. But it does not follow that 'having the right time' is meaningless, it just means that we do not have sufficient information to decide which, if any, of the frames really does have the right time.
Perhaps Born's argument is that such information is unobtainable in principle because the laws of nature do not contain any parameter expressing any lack of symmetry in the propagation of light. This is an important point which requires further analysis.
First, it should be emphasized that in this context the "laws of nature" can only refer to laws that do not rely on the concept of distant simultaneity, since this is the very concept Born is seeking to define. In particular, the constancy of the one-way speed of light is not included in those laws.
Second, the relevant laws of nature are to a large extent based on observations and experiments in terrestrial laboratories, in which the conditions in which light is emitted and propagates may well be constant, and this may be the reason why those laws do not contain any parameter determining the presence or absence of symmetry.
For example, according to a more modern theory of light propagation than the ether model, electromagnetic radiation can be regarded as outwardly propagating disturbances in the electric fields of charged particles. Such disturbances may, for example, be caused by sudden, local accelerations of those particles - see for example Lesson 4 in this document by Daniel V. Schroeder. In this model, any light source carries the field in which the light propagates around with itself. Light emitted by a source that is stationary on Earth thus propagates in constant and quite possibly broadly symmetrical conditions in different directions, regardless of, for example, the position of the Earth in its orbit around the sun.
The "local acceleration history" of a source of light could thus be a parameter which is missing from the laws of nature as currently formulated and which may help to determine whether or not the conditions in which light propagates in opposite directions from that source are symmetrical.
Nevertheless, it may well be that from the point of view of a charge that has undergone local acceleration, for example as a result of a collision, everything still looks symmetrical in its new frame of reference and that thus "local acceleration history" is not directly observable. Worse, it may be difficult or impossible to reconstruct such acceleration histories if we do not already have a frame of reference which we know to be symmetrical and which we can thus use to define simultaneity.
If that is so - and I will have to look into these issues in much greater detail in subsequent posts on alternative definitions and theories that are compatible with observation and experiment - then Einstein's clock adjustment procedure may be justified on pragmatic grounds as a procedure that yields simple laws and enables accurate predictions, as long as it is made clear that it is not a synchronization procedure.
In summary, Born raises an important issue, which is the detectability of asymmetrical conditions in the emission or propagation of light, although he only does so in relation to the outmoded ether theory of light. His point that there may be no practical alternative to Einstein's clock adjustment procedure if there is no such detectability deserves careful consideration. On the other hand, Born fails to make a convincing case for the claim that Einstein's clock adjustment procedure is a synchronization procedure in all uniformly moving frames of reference.
So, what led Born to believe that Einstein's clock adjustment procedure can function as a synchronization procedure? I think the main reason is that he took it for granted that the one-way speed of light is constant for all observers. As he puts it at the start of his chapter on simultaneity, 'experience teaches us that the speed of light always has the same value c, regardless of the state of motion of the observer', and this fact requires us to drop 'the principles of defining space and time as they have always been applied until now'. (p. 194) In reality, of course, defining space and time, and in particular distant simultaneity, is a step that comes before experience can tell us anything about the constancy of c for all observers.
Born's approach of using the constancy of c as his starting point is reminiscent of Einstein's desire to adjust clocks in such a way that Maxwell's laws, and thus the constancy of c, are valid in all frames of reference. Neither of these physicists seems to have been interested primarily in exploring how clocks need to be adjusted in order to arrive at a meaningful definition of simultaneity. The result, I fear, is a theory in which clocks are not synchronized and consequently concepts that rely on synchronization, such as distant simultaneity, one-way speed and causality, break down.
Einstein's and Born's writings thus raise an intriguing possibility: that the strangeness of special relativity does not correspond to anything in the observed phenomena but is purely the result of a clock adjustment procedure which is not a synchronization procedure. In other words, the world may not actually be half as weird as a superficial reading of some physics books might suggest.
For now, however, this is merely a hypothesis which requires further testing against some of the more recent specialized literature on time and simultaneity in physics, starting with writings on these issues by Max Jammer and Allen Janis - in my next post.
This blog is motivated by my desire to understand the special theory of relativity, in particular the principle of the constancy of the speed of light for every observer. How did physicists come to accept it? Is it based on convention, theory or observation? Are there any alternative conventions or theories that are compatible with observation and experiment?
Thursday, 3 March 2011
Monday, 10 January 2011
Einstein and time - the plot is thickening
How did Einstein justify his clock adjustment procedure using light signals? And how did he justify the idea that it represents a synchronization procedure not just in some frames of reference but in any frame in which the laws of mechanics hold?
These questions are important because some of the strangest claims of special relativity - as detailed in my previous post - are a direct result of Einstein's clock adjustment procedure and the idea that it represents a synchronization procedure in all such frames of reference.
In his 1905 article "On the Electrodynamics of Moving Bodies", Einstein set out a clock adjustment procedure which, according to him, invariably results in synchronized clocks in separate locations.
According to Einstein (p. 894), a time that is common to a location A in a coordinate system in which Newton's laws of mechanics hold and a location B in the same coordinate system can be defined 'by stipulating by definition that the time it takes for light to travel from A to B is the same as the time it takes for it to travel from B to A. For, let a ray of light leave A at "A time" tA in the direction of B, let it be reflected in B at "B time" tB in the direction of A and let it arrive back in A at "A time" t'A. The two clocks are defined to be synchronous if
tB – tA = t'A – tB. … '
What Einstein describes here is how, given a first clock in location A, a light signal can be used to adjust a second clock in location B such that the signal arrival time in B lies in the middle between the signal departure and arrival times in A. Einstein then effectively says that clocks adjusted in this way can be declared to be synchronous as a matter of definition. He thus suggests that there is no substance to the concept of simultaneity other than the existence of some systematic procedure to adjust distant clocks.
This position is made more explicit in Einstein's 1916 book, in which he approvingly cites a fictitious participant in a dialogue on simultaneity as saying: "There is only one demand to be made of the definition of simultaneity, namely, that in every real case it must supply us with an empirical decision as to whether or not the conception that has to be defined is fulfilled."
In these writings, Einstein thus fails to distinguish between clock adjustment procedures, which may indeed be chosen arbitrarily, and synchronization procedures, which must in fact meet additional criteria, as I have previously shown with reference to sound signals in this and this post.
That is not to say that Einstein did not have any reason to opt for his clock adjustment procedure. The chief reason, it seems, is his stated aim "to arrive at a simple and consistent electrodynamics of moving bodies on the basis of Maxwell's theory for bodies at rest" ("On the Electrodynamics of Moving Bodies", p. 892). In Maxwell's theory, light travels at c in all directions, and generalizing this theory to all frames of reference therefore requires a clock adjustment procedure which ensures that the speed of light is always identical in opposite directions.
While this may well explain Einstein's choice of clock adjustment procedure, it doesn't make that procedure a synchronization procedure. Indeed, both of the criteria that I have identified for a clock adjustment procedure using Einstein's signalling method to qualify as a synchronization procedure appear to be violated.
First, as observed before, Einstein's clock adjustment procedure leads to the theoretical possibility of signals arriving at their destination before they were emitted.
Second, I have suggested that Einstein's clock adjustment procedure is a synchronization procedure only if the conditions in which the signals propagate are symmetrical in opposite directions. This needs to be qualified a little bit. Strictly speaking this is a sufficient rather than a necessary condition, since it may turn out that signals that do not propagate in identical conditions in opposite directions nevertheless lead to the same clock adjustment if the effects of various parameters that are different in different directions cancel each other out. Nevertheless, I would suggest that equal conditions of signal emission as well as propagation in opposite directions should be made a requirement of any (primary) Einstein-like synchronization procedure so that we can be sure that the signal used is suitable.
But if this condition is fulfilled for particular light signals in a particular frame of reference, then the same light signals cannot be used to synchronize clocks in a second frame of reference that moves relative to the first. Let me illustrate the situation with a diagram:
In this diagram, in a frame of reference in which the laws of mechanics hold, some kind of signal - objects projected by an explosion, sound, light or any other signal - is emitted. This event, represented by the star, occurs just as an observer A in a second frame of reference passes by. Suppose that the conditions in which the signal is emitted and propagates are completely symmetrical in all directions in the first frame of reference, and that thus Einstein's synchronization procedure is applicable, producing equal speeds of propagation in opposite directions in that frame.
My contention is that, regardless of the kind of signal used, the same signal cannot then be used to synchronize clocks in A's frame of reference, since A's movement in one of the directions in which the signal propagates means that the symmetry of the conditions in which it is emitted or propagates is inevitably broken.
Now suppose that the same kind of signal is sent out from A at the same time as the first signal, and that empirically it is found to travel in all directions at the same one-way speed (as defined in this post) as the first signal:
Then the second signal cannot be used to synchronize clocks in A's frame of reference, either, since we already know that the first signal cannot be used. This kind of reasoning is completely uncontroversial in the case of, for example, objects projected by an explosion or sound. Surely light cannot be an exception.
Or can it? In a book published in 1962 in English and two years later in German, the physicist Max Born argues that the absence of a universal light medium, or ether, which was already noted by Einstein in 1905, means that each frame of reference in which the laws of mechanics hold is equivalent to any other as far as the propagation of light is concerned and that therefore Einstein's clock adjustment procedure can function as a synchronization procedure in every frame of reference.
Born's reasoning as set out in his book is one of the most detailed attempts to justify the idea that Einstein's clock adjustment procedure is a synchronization procedure that I have found in the literature. It therefore requires very careful analysis - in my next post.
These questions are important because some of the strangest claims of special relativity - as detailed in my previous post - are a direct result of Einstein's clock adjustment procedure and the idea that it represents a synchronization procedure in all such frames of reference.
In his 1905 article "On the Electrodynamics of Moving Bodies", Einstein set out a clock adjustment procedure which, according to him, invariably results in synchronized clocks in separate locations.
According to Einstein (p. 894), a time that is common to a location A in a coordinate system in which Newton's laws of mechanics hold and a location B in the same coordinate system can be defined 'by stipulating by definition that the time it takes for light to travel from A to B is the same as the time it takes for it to travel from B to A. For, let a ray of light leave A at "A time" tA in the direction of B, let it be reflected in B at "B time" tB in the direction of A and let it arrive back in A at "A time" t'A. The two clocks are defined to be synchronous if
tB – tA = t'A – tB. … '
What Einstein describes here is how, given a first clock in location A, a light signal can be used to adjust a second clock in location B such that the signal arrival time in B lies in the middle between the signal departure and arrival times in A. Einstein then effectively says that clocks adjusted in this way can be declared to be synchronous as a matter of definition. He thus suggests that there is no substance to the concept of simultaneity other than the existence of some systematic procedure to adjust distant clocks.
This position is made more explicit in Einstein's 1916 book, in which he approvingly cites a fictitious participant in a dialogue on simultaneity as saying: "There is only one demand to be made of the definition of simultaneity, namely, that in every real case it must supply us with an empirical decision as to whether or not the conception that has to be defined is fulfilled."
In these writings, Einstein thus fails to distinguish between clock adjustment procedures, which may indeed be chosen arbitrarily, and synchronization procedures, which must in fact meet additional criteria, as I have previously shown with reference to sound signals in this and this post.
That is not to say that Einstein did not have any reason to opt for his clock adjustment procedure. The chief reason, it seems, is his stated aim "to arrive at a simple and consistent electrodynamics of moving bodies on the basis of Maxwell's theory for bodies at rest" ("On the Electrodynamics of Moving Bodies", p. 892). In Maxwell's theory, light travels at c in all directions, and generalizing this theory to all frames of reference therefore requires a clock adjustment procedure which ensures that the speed of light is always identical in opposite directions.
While this may well explain Einstein's choice of clock adjustment procedure, it doesn't make that procedure a synchronization procedure. Indeed, both of the criteria that I have identified for a clock adjustment procedure using Einstein's signalling method to qualify as a synchronization procedure appear to be violated.
First, as observed before, Einstein's clock adjustment procedure leads to the theoretical possibility of signals arriving at their destination before they were emitted.
Second, I have suggested that Einstein's clock adjustment procedure is a synchronization procedure only if the conditions in which the signals propagate are symmetrical in opposite directions. This needs to be qualified a little bit. Strictly speaking this is a sufficient rather than a necessary condition, since it may turn out that signals that do not propagate in identical conditions in opposite directions nevertheless lead to the same clock adjustment if the effects of various parameters that are different in different directions cancel each other out. Nevertheless, I would suggest that equal conditions of signal emission as well as propagation in opposite directions should be made a requirement of any (primary) Einstein-like synchronization procedure so that we can be sure that the signal used is suitable.
But if this condition is fulfilled for particular light signals in a particular frame of reference, then the same light signals cannot be used to synchronize clocks in a second frame of reference that moves relative to the first. Let me illustrate the situation with a diagram:
In this diagram, in a frame of reference in which the laws of mechanics hold, some kind of signal - objects projected by an explosion, sound, light or any other signal - is emitted. This event, represented by the star, occurs just as an observer A in a second frame of reference passes by. Suppose that the conditions in which the signal is emitted and propagates are completely symmetrical in all directions in the first frame of reference, and that thus Einstein's synchronization procedure is applicable, producing equal speeds of propagation in opposite directions in that frame.
My contention is that, regardless of the kind of signal used, the same signal cannot then be used to synchronize clocks in A's frame of reference, since A's movement in one of the directions in which the signal propagates means that the symmetry of the conditions in which it is emitted or propagates is inevitably broken.
Now suppose that the same kind of signal is sent out from A at the same time as the first signal, and that empirically it is found to travel in all directions at the same one-way speed (as defined in this post) as the first signal:
Then the second signal cannot be used to synchronize clocks in A's frame of reference, either, since we already know that the first signal cannot be used. This kind of reasoning is completely uncontroversial in the case of, for example, objects projected by an explosion or sound. Surely light cannot be an exception.
Or can it? In a book published in 1962 in English and two years later in German, the physicist Max Born argues that the absence of a universal light medium, or ether, which was already noted by Einstein in 1905, means that each frame of reference in which the laws of mechanics hold is equivalent to any other as far as the propagation of light is concerned and that therefore Einstein's clock adjustment procedure can function as a synchronization procedure in every frame of reference.
Born's reasoning as set out in his book is one of the most detailed attempts to justify the idea that Einstein's clock adjustment procedure is a synchronization procedure that I have found in the literature. It therefore requires very careful analysis - in my next post.
Tuesday, 7 December 2010
Einstein's clock procedure in the literature
According to the principle of the constancy of the speed of light in SR, if an observer chases after a flash of light, the light will keep moving away from the observer at the universal speed c no matter how much the observer speeds up. Likewise, if an observer runs into a flash of light, the light will keep moving towards the observer at c no matter how much the observer speeds up.
As I mentioned in a previous post, another consequence of the constancy of c is the possibility of causality paradoxes if hypothetical superluminal signals are considered. But at low speeds, too, there are some surprising effects. For example, if two observers A and B at rest relative to each other at opposite ends of the observable universe started to walk in the same direction A--> B--> at the same time, then, in accordance with the transformations of SR, A would suddenly have to consider that B set out 300 years earlier than A and is now long dead. If both stopped after a few metres, however, B would promptly come back to life as far as A is concerned since A would now consider that A and B set out at the same time, after all, and also stopped at the same time.
All this strangeness is at least partly the making of physicists because, as explained in previous posts, the notions of "simultaneity" and "one-way speed" as defined in SR crucially depend on Einstein's choice of clock adjustment procedure. It is now time to look at the literature on SR to see how physicists have justified such a clock adjustment procedure, and how they have defended the idea that it represents a synchronization procedure that may serve to define simultaneity and one-way speed.
Let me begin with a little survey of the texts I would like to examine. The first two are Albert Einstein's famous 1905 article "On the Electrodynamics of Moving Bodies" and his subsequent account of the main features of SR intended for a wider audience, first published in 1916. In my opinion, these two publications are much clearer regarding the foundations of special relativity than many other texts published on the subject since. In particular, Einstein is perfectly lucid on the role of convention, definition or stipulation in his theory. On the other hand, there is very little in these texts to motivate or justify his clock adjustment procedure, let alone the idea that it may serve as a synchronization procedure.
This is perhaps unsurprising since, as far as I know, Einstein was addressing an audience whose main concern was to reconcile recent experimental results with the erroneous idea of an essentially static, all-pervasive medium for light, or "ether". He was not writing for future generations of students of physics who had never had any reason to believe in such an "ether" in the first place and were much more interested in the issue of meaningful synchronization procedures.
This is where modern textbooks and other publications focusing on the foundations of special relativity come in. Two which I would like to consider are an online article by Allen Janis wholly dedicated to the issue of the "Conventionality of Simultaneity" in SR, and a 1977 article by Reza Mansouri and Roman U. Sexl on "A Test Theory of Special Relativity: I. Simultaneity and Clock Synchronization". In addition, I have identified four books which are of particular interest to me because of their explicit emphasis on the concepts underlying SR: Leo Sartori's Understanding Relativity (1996); Wolfgang Rindler's Relativity: Special, General, Cosmological (2001); Vesselin Petkov's Relativity and the Nature of Spacetime (2005); and above all Kevin Brown's Reflections on Relativity (2010).
Kevin Brown's book is particularly relevant to my project because it explicitly addresses some of the very same issues I am grappling with in this blog. What is more, it gives a clear, coherent and erudite account of the foundations of SR unrivalled by any of the other texts I have mentioned. If there is hope for my understanding of the principle of the constancy of c, it lies in Kevin Brown's book!
But first things first, so let me start with Brown's illustrious precursor, Albert Einstein - in my next post.
As I mentioned in a previous post, another consequence of the constancy of c is the possibility of causality paradoxes if hypothetical superluminal signals are considered. But at low speeds, too, there are some surprising effects. For example, if two observers A and B at rest relative to each other at opposite ends of the observable universe started to walk in the same direction A--> B--> at the same time, then, in accordance with the transformations of SR, A would suddenly have to consider that B set out 300 years earlier than A and is now long dead. If both stopped after a few metres, however, B would promptly come back to life as far as A is concerned since A would now consider that A and B set out at the same time, after all, and also stopped at the same time.
All this strangeness is at least partly the making of physicists because, as explained in previous posts, the notions of "simultaneity" and "one-way speed" as defined in SR crucially depend on Einstein's choice of clock adjustment procedure. It is now time to look at the literature on SR to see how physicists have justified such a clock adjustment procedure, and how they have defended the idea that it represents a synchronization procedure that may serve to define simultaneity and one-way speed.
Let me begin with a little survey of the texts I would like to examine. The first two are Albert Einstein's famous 1905 article "On the Electrodynamics of Moving Bodies" and his subsequent account of the main features of SR intended for a wider audience, first published in 1916. In my opinion, these two publications are much clearer regarding the foundations of special relativity than many other texts published on the subject since. In particular, Einstein is perfectly lucid on the role of convention, definition or stipulation in his theory. On the other hand, there is very little in these texts to motivate or justify his clock adjustment procedure, let alone the idea that it may serve as a synchronization procedure.
This is perhaps unsurprising since, as far as I know, Einstein was addressing an audience whose main concern was to reconcile recent experimental results with the erroneous idea of an essentially static, all-pervasive medium for light, or "ether". He was not writing for future generations of students of physics who had never had any reason to believe in such an "ether" in the first place and were much more interested in the issue of meaningful synchronization procedures.
This is where modern textbooks and other publications focusing on the foundations of special relativity come in. Two which I would like to consider are an online article by Allen Janis wholly dedicated to the issue of the "Conventionality of Simultaneity" in SR, and a 1977 article by Reza Mansouri and Roman U. Sexl on "A Test Theory of Special Relativity: I. Simultaneity and Clock Synchronization". In addition, I have identified four books which are of particular interest to me because of their explicit emphasis on the concepts underlying SR: Leo Sartori's Understanding Relativity (1996); Wolfgang Rindler's Relativity: Special, General, Cosmological (2001); Vesselin Petkov's Relativity and the Nature of Spacetime (2005); and above all Kevin Brown's Reflections on Relativity (2010).
Kevin Brown's book is particularly relevant to my project because it explicitly addresses some of the very same issues I am grappling with in this blog. What is more, it gives a clear, coherent and erudite account of the foundations of SR unrivalled by any of the other texts I have mentioned. If there is hope for my understanding of the principle of the constancy of c, it lies in Kevin Brown's book!
But first things first, so let me start with Brown's illustrious precursor, Albert Einstein - in my next post.
Sunday, 7 November 2010
More on sound, light and time
So, in what sense does the application of the Einstein clock adjustment procedure to sound signals lead to nonsensical results, and why?
As we have seen, it leads for example to the result that walking speeds become infinitely fast in some frames of reference, and that, by speeding up a little bit more, it becomes possible to walk into the past in such frames. The concepts of one-way speed and causality thus break down. In purely mathematical terms, people would even be able to cause serious causality paradoxes by walking into the past and then turning round and arriving back home before they left. Of course, this is not actually possible because it would be physically impossible to move back at a sufficiently high speed - ultimately because the mathematical "plane of simultaneity" defined by such a clock adjustment procedure is not actually a plane of simultaneity at all. The concept of simultaneity thus breaks down.
It therefore seems that the Einstein synchronization procedure cannot be applied to sound signals. But what about the idea that synchronization is just a matter of definition? In other words, prior to deciding on a synchronization procedure, how can we know that, from the point of view of an observer moving relative to a body of air, the one-way speed of sound is not equal in different directions?
First, we can use a limited concept of one-way speed that is independent of any synchronization procedure: the one-way speed of a first signal sent out from A is higher, equal to or lower than that of a second signal sent out from A at the same time if the first signal arrives in B before, at the same time as or after the second, respectively. Clocks in A and B do not need to be synchronized to make such observations. The concept of one-way speed in a single direction is thus well-defined in comparative terms - lower, equal or higher - regardless of any synchronization procedure.
Now consider an observer A who is stationary with respect to a body of air. This observer will find empirically that different signals sent out from A, including sound signals, exhibit the same relative one-way speeds as defined above regardless of the direction in which they are sent out. An observer B moving relative to the same stationary body of air, however, will find that sound signals sent out from B in the "forward" direction travel more slowly compared to the same range of other signals sent out from B, while sound signals sent out in the "backward" direction travel faster compared to the same range of other signals. The second observer thus has good reasons to conclude on empirical grounds that the one-way speed of sound is not equal in the forward and backward directions even prior to defining any synchronization procedure.
But there is more. Our theoretical knowledge of how sound waves propagate, too, tells us that, for an observer travelling relative to a body of air, the one-way speeds of sound in the forward and backward directions cannot be equal. We know, for example, that sound consists of outwardly propagating vibrations of air molecules. This means that, for an observer who is stationary relative to a body of air, the conditions in which sound propagates are symmetrical in all directions, while for an observer moving relative to a body of air the conditions in which sound propagates are not symmetrical. We can therefore expect the one-way speed of sound to be equal in different directions for the first observer and unequal for the second.
And there is even more. For any signal, if we believe, assume or stipulate that the conditions in which it propagates are symmetrical for a given observer, then it is difficult to see how they can also be symmetrical for a second observer who is moving relative to the first. This seems fundamental to me and it goes to the heart of my difficulties in getting to grips with the special theory of relativity.
I have no particular problem with the idea that acceleration may lead to the slowing down of clocks or even the contraction of measuring rods. The empirical finding that the two-way speed of light is always measured as c, if indeed there is such an empirical finding, is somewhat surprising but may be explicable precisely as a result of the effects of acceleration on clocks and measuring rods - in fact, if there are such effects, we may choose to correct for them by adjusting the rate at which clocks that have undergone acceleration tick, resulting in the two-way speed not always being measured as c.
But what I cannot yet fathom is on what grounds generations of physicists have seen fit to declare that, if the conditions in which light propagates are deemed to be symmetrical relative to a source of light, the one-way speed of light is deemed to be the same in all directions even for an observer who is moving relative to that source of light. Or why they would want to adjust clocks in such a way that it is made to be the same in all directions for such an observer.
What I have endeavoured to show thus far is that, while of course physicists are free to adjust clocks in this way, they are not free to declare that such a clock adjustment procedure is a synchronization procedure. And that if it isn't the concepts of simultaneity, one-way speed and causality may be undermined. Ultimately, then, it may turn out that special relativity is certainly a usable theory in that it successfully predicts the outcome of experiments, but that it relies on a clock adjustment procedure which is not a synchronization procedure and that therefore the concepts of one-way speed, simultaneity and causality have limited applicability in the framework of that theory.
I think it is now time for a few propositions relating to the role played by definition or stipulation in the principle of the constancy of the speed of light for every observer in the special theory of relativity.
P1: The constancy of the two-way speed of light in every coordinate system in which the laws of mechanics hold is an empirical matter once the rate at which clocks in different such coordinate systems tick has been set.
P2: The constancy of the one-way speed of light in every direction in every coordinate system in which the laws of mechanics hold is an empirical matter once a synchronization procedure for clocks in different locations in different such coordinate systems has been decided on.
P3: Not every clock adjustment procedure is a clock synchronization procedure.
P4: A clock adjustment procedure resulting in clock settings under which a signal sent from a location A may arrive in a location B "before it was sent" is not a synchronization procedure.
P5: A clock adjustment procedure that relies on sending a signal from location A to B and back and sets the signal arrival time in B to be in the middle between the signal sending and arrival times in A is a synchronization procedure only if the conditions in which the signal propagates are symmetrical in both directions.
So, is the Einstein clock adjustment procedure using light signals a synchronization procedure? On the face of it it is difficult to see how it can be, but once again, the answer depends on a number of empirical and theoretical issues which I have yet to look into in any detail over the months and years to come.
Before I embark on this quest, I think it's high time I started reviewing what the physics literature has to say on the role of definition or stipulation in the principle of the constancy of the speed of light for every observer - in my next blog post.
As we have seen, it leads for example to the result that walking speeds become infinitely fast in some frames of reference, and that, by speeding up a little bit more, it becomes possible to walk into the past in such frames. The concepts of one-way speed and causality thus break down. In purely mathematical terms, people would even be able to cause serious causality paradoxes by walking into the past and then turning round and arriving back home before they left. Of course, this is not actually possible because it would be physically impossible to move back at a sufficiently high speed - ultimately because the mathematical "plane of simultaneity" defined by such a clock adjustment procedure is not actually a plane of simultaneity at all. The concept of simultaneity thus breaks down.
It therefore seems that the Einstein synchronization procedure cannot be applied to sound signals. But what about the idea that synchronization is just a matter of definition? In other words, prior to deciding on a synchronization procedure, how can we know that, from the point of view of an observer moving relative to a body of air, the one-way speed of sound is not equal in different directions?
First, we can use a limited concept of one-way speed that is independent of any synchronization procedure: the one-way speed of a first signal sent out from A is higher, equal to or lower than that of a second signal sent out from A at the same time if the first signal arrives in B before, at the same time as or after the second, respectively. Clocks in A and B do not need to be synchronized to make such observations. The concept of one-way speed in a single direction is thus well-defined in comparative terms - lower, equal or higher - regardless of any synchronization procedure.
Now consider an observer A who is stationary with respect to a body of air. This observer will find empirically that different signals sent out from A, including sound signals, exhibit the same relative one-way speeds as defined above regardless of the direction in which they are sent out. An observer B moving relative to the same stationary body of air, however, will find that sound signals sent out from B in the "forward" direction travel more slowly compared to the same range of other signals sent out from B, while sound signals sent out in the "backward" direction travel faster compared to the same range of other signals. The second observer thus has good reasons to conclude on empirical grounds that the one-way speed of sound is not equal in the forward and backward directions even prior to defining any synchronization procedure.
But there is more. Our theoretical knowledge of how sound waves propagate, too, tells us that, for an observer travelling relative to a body of air, the one-way speeds of sound in the forward and backward directions cannot be equal. We know, for example, that sound consists of outwardly propagating vibrations of air molecules. This means that, for an observer who is stationary relative to a body of air, the conditions in which sound propagates are symmetrical in all directions, while for an observer moving relative to a body of air the conditions in which sound propagates are not symmetrical. We can therefore expect the one-way speed of sound to be equal in different directions for the first observer and unequal for the second.
And there is even more. For any signal, if we believe, assume or stipulate that the conditions in which it propagates are symmetrical for a given observer, then it is difficult to see how they can also be symmetrical for a second observer who is moving relative to the first. This seems fundamental to me and it goes to the heart of my difficulties in getting to grips with the special theory of relativity.
I have no particular problem with the idea that acceleration may lead to the slowing down of clocks or even the contraction of measuring rods. The empirical finding that the two-way speed of light is always measured as c, if indeed there is such an empirical finding, is somewhat surprising but may be explicable precisely as a result of the effects of acceleration on clocks and measuring rods - in fact, if there are such effects, we may choose to correct for them by adjusting the rate at which clocks that have undergone acceleration tick, resulting in the two-way speed not always being measured as c.
But what I cannot yet fathom is on what grounds generations of physicists have seen fit to declare that, if the conditions in which light propagates are deemed to be symmetrical relative to a source of light, the one-way speed of light is deemed to be the same in all directions even for an observer who is moving relative to that source of light. Or why they would want to adjust clocks in such a way that it is made to be the same in all directions for such an observer.
What I have endeavoured to show thus far is that, while of course physicists are free to adjust clocks in this way, they are not free to declare that such a clock adjustment procedure is a synchronization procedure. And that if it isn't the concepts of simultaneity, one-way speed and causality may be undermined. Ultimately, then, it may turn out that special relativity is certainly a usable theory in that it successfully predicts the outcome of experiments, but that it relies on a clock adjustment procedure which is not a synchronization procedure and that therefore the concepts of one-way speed, simultaneity and causality have limited applicability in the framework of that theory.
I think it is now time for a few propositions relating to the role played by definition or stipulation in the principle of the constancy of the speed of light for every observer in the special theory of relativity.
P1: The constancy of the two-way speed of light in every coordinate system in which the laws of mechanics hold is an empirical matter once the rate at which clocks in different such coordinate systems tick has been set.
P2: The constancy of the one-way speed of light in every direction in every coordinate system in which the laws of mechanics hold is an empirical matter once a synchronization procedure for clocks in different locations in different such coordinate systems has been decided on.
P3: Not every clock adjustment procedure is a clock synchronization procedure.
P4: A clock adjustment procedure resulting in clock settings under which a signal sent from a location A may arrive in a location B "before it was sent" is not a synchronization procedure.
P5: A clock adjustment procedure that relies on sending a signal from location A to B and back and sets the signal arrival time in B to be in the middle between the signal sending and arrival times in A is a synchronization procedure only if the conditions in which the signal propagates are symmetrical in both directions.
So, is the Einstein clock adjustment procedure using light signals a synchronization procedure? On the face of it it is difficult to see how it can be, but once again, the answer depends on a number of empirical and theoretical issues which I have yet to look into in any detail over the months and years to come.
Before I embark on this quest, I think it's high time I started reviewing what the physics literature has to say on the role of definition or stipulation in the principle of the constancy of the speed of light for every observer - in my next blog post.
Tuesday, 21 September 2010
How to use sound to do things with time
I know it’s been a long time, but what do you do if the choice is between exploring the deepest mysteries of the universe and doing domestic chores? The latter of course because it’s a necessity.
So, once again, to what extent is the idea that the speed of light is the same for every observer based on convention, stipulation or definition rather than theory or empirical fact? As we’ve seen, according to Einstein the constancy of c is partly a matter of definition. In his 1905 article "On the Electrodynamics of Moving Bodies", he said we are free to define simultaneity in different points in such a way that the speed of light is always the same in opposite directions.
At first sight, this seems an astonishing thing to say in view of the empirical fact that, if a source of light moves relative to the laboratory near the speed of light, then light seems to move more slowly away from that source in the “forward” direction than it does in the “backward” direction, just like the sound caused by an aircraft flying near the speed of sound moves more slowly away from the nose of the aircraft than it does from the tail of the aircraft.
However, the “empirical fact” just cited depends on measurements of the one-way speed of light in the “forward” and the “backward” direction. Einstein correctly observes that, in order to measure such one-way speeds, we first need a definition of simultaneity in different points or, which amounts to the same thing, a procedure to synchronize clocks in different points. Einstein then says that we are free to synchronize clocks in different points in such a way that the speed of light always turns out to be the same in opposite directions.
This raises an interesting question: by applying the Einstein clock adjustment procedure to sound signals, is it possible to make the speed of sound relative to an aircraft flying at subsonic speed the same in the “forward” and “backward” directions, too?
My answer is that, yes, technically that can be done, but it turns out that the Einstein clock adjustment procedure applied to sound is not a synchronization procedure. It therefore leaves us without any meaningful concept of simultaneity and, as a result, the concepts of one-way speed and of cause and effect applied to signals become meaningless, too.
To see this in greater detail, I’ve worked out the transformations between the coordinate systems S1 and S2 of two observers moving at subsonic speeds v1 and v2 relative to an undisturbed body of air S0 using the Einstein clock adjustment procedure described in my previous post, but applied to sound moving at the two-way speed of vs in S0, rather than to light signals.
Without going into details, suffice it to say that the way I have derived the transformation formulas is based on the known empirical facts concerning the two-way speed of sound in S0, S1 and S2 and the known behaviour of single clocks and measuring rods moving at subsonic speeds in S0. The result I’ve arrived at is that, in standard configuration - in other words if (0, 0) in S1 coincides with (0, 0) in S2 - for any pair of coordinates (x, t) in S1, the coordinates (x', t') in S2 are
(1)
(2)
where
and
What I find striking about this result is its similarity with the Lorentz transformation of special relativity, according to which
and
where
Of particular significance is the presence of the term
in (2), which corresponds to
in the Lorentz transformation, where it is responsible for the causality "paradoxes" that arise in special relativity if hypothetical signals moving at superluminal speeds are considered.
As equation (2) shows, very similar "paradoxes" result with supersonic signals if we apply the Einstein clock adjustment procedure to sound. For example, if we consider the case of v1 = 0 and imagine a plane flying at v2 through S0, we can arrange for the nose of the plane to be millions of years "in the past" compared to the tail from the point of view of a passenger travelling on the plane provided v2 is sufficiently close to the speed of sound. So, passengers at the tail of the plane could travel into the distant "past" in terms of their S2-coordinates just by sauntering over to the nose. It turns out that doing so requires the passengers to travel at supersonic speeds relative to S0. In fact the condition that signal speeds u in S0 must meet if a signal sent out from a point in S2 is to arrive at a different point in S2 "before it was sent" is of the same form as in special relativity:
Other odd effects result if we let these passengers saunter back to the tail of the plane: in terms of S2 coordinates, however fast they walk or run, they would take millions of years to get back to the tail of the plane while only ageing by a few seconds, making for extreme "time dilation" during their journey.
None of this is really paradoxical - the way we adjust our clocks cannot result in any true paradoxes - it is just utterly nonsensical. Just in what sense it is nonsensical, and what this means for the Einstein synchronization procedure applied to light signals, will require careful analysis and interpretation - in my next post.
So, once again, to what extent is the idea that the speed of light is the same for every observer based on convention, stipulation or definition rather than theory or empirical fact? As we’ve seen, according to Einstein the constancy of c is partly a matter of definition. In his 1905 article "On the Electrodynamics of Moving Bodies", he said we are free to define simultaneity in different points in such a way that the speed of light is always the same in opposite directions.
At first sight, this seems an astonishing thing to say in view of the empirical fact that, if a source of light moves relative to the laboratory near the speed of light, then light seems to move more slowly away from that source in the “forward” direction than it does in the “backward” direction, just like the sound caused by an aircraft flying near the speed of sound moves more slowly away from the nose of the aircraft than it does from the tail of the aircraft.
However, the “empirical fact” just cited depends on measurements of the one-way speed of light in the “forward” and the “backward” direction. Einstein correctly observes that, in order to measure such one-way speeds, we first need a definition of simultaneity in different points or, which amounts to the same thing, a procedure to synchronize clocks in different points. Einstein then says that we are free to synchronize clocks in different points in such a way that the speed of light always turns out to be the same in opposite directions.
This raises an interesting question: by applying the Einstein clock adjustment procedure to sound signals, is it possible to make the speed of sound relative to an aircraft flying at subsonic speed the same in the “forward” and “backward” directions, too?
My answer is that, yes, technically that can be done, but it turns out that the Einstein clock adjustment procedure applied to sound is not a synchronization procedure. It therefore leaves us without any meaningful concept of simultaneity and, as a result, the concepts of one-way speed and of cause and effect applied to signals become meaningless, too.
To see this in greater detail, I’ve worked out the transformations between the coordinate systems S1 and S2 of two observers moving at subsonic speeds v1 and v2 relative to an undisturbed body of air S0 using the Einstein clock adjustment procedure described in my previous post, but applied to sound moving at the two-way speed of vs in S0, rather than to light signals.
Without going into details, suffice it to say that the way I have derived the transformation formulas is based on the known empirical facts concerning the two-way speed of sound in S0, S1 and S2 and the known behaviour of single clocks and measuring rods moving at subsonic speeds in S0. The result I’ve arrived at is that, in standard configuration - in other words if (0, 0) in S1 coincides with (0, 0) in S2 - for any pair of coordinates (x, t) in S1, the coordinates (x', t') in S2 are
(1)
(2)
where
and
What I find striking about this result is its similarity with the Lorentz transformation of special relativity, according to which
and
where
Of particular significance is the presence of the term
in (2), which corresponds to
in the Lorentz transformation, where it is responsible for the causality "paradoxes" that arise in special relativity if hypothetical signals moving at superluminal speeds are considered.
As equation (2) shows, very similar "paradoxes" result with supersonic signals if we apply the Einstein clock adjustment procedure to sound. For example, if we consider the case of v1 = 0 and imagine a plane flying at v2 through S0, we can arrange for the nose of the plane to be millions of years "in the past" compared to the tail from the point of view of a passenger travelling on the plane provided v2 is sufficiently close to the speed of sound. So, passengers at the tail of the plane could travel into the distant "past" in terms of their S2-coordinates just by sauntering over to the nose. It turns out that doing so requires the passengers to travel at supersonic speeds relative to S0. In fact the condition that signal speeds u in S0 must meet if a signal sent out from a point in S2 is to arrive at a different point in S2 "before it was sent" is of the same form as in special relativity:
Other odd effects result if we let these passengers saunter back to the tail of the plane: in terms of S2 coordinates, however fast they walk or run, they would take millions of years to get back to the tail of the plane while only ageing by a few seconds, making for extreme "time dilation" during their journey.
None of this is really paradoxical - the way we adjust our clocks cannot result in any true paradoxes - it is just utterly nonsensical. Just in what sense it is nonsensical, and what this means for the Einstein synchronization procedure applied to light signals, will require careful analysis and interpretation - in my next post.
Subscribe to:
Posts (Atom)