I know it’s been a long time, but what do you do if the choice is between exploring the deepest mysteries of the universe and doing domestic chores? The latter of course because it’s a necessity.
So, once again, to what extent is the idea that the speed of light is the same for every observer based on convention, stipulation or definition rather than theory or empirical fact? As we’ve seen, according to Einstein the constancy of c is partly a matter of definition. In his 1905 article "On the Electrodynamics of Moving Bodies", he said we are free to define simultaneity in different points in such a way that the speed of light is always the same in opposite directions.
At first sight, this seems an astonishing thing to say in view of the empirical fact that, if a source of light moves relative to the laboratory near the speed of light, then light seems to move more slowly away from that source in the “forward” direction than it does in the “backward” direction, just like the sound caused by an aircraft flying near the speed of sound moves more slowly away from the nose of the aircraft than it does from the tail of the aircraft.
However, the “empirical fact” just cited depends on measurements of the one-way speed of light in the “forward” and the “backward” direction. Einstein correctly observes that, in order to measure such one-way speeds, we first need a definition of simultaneity in different points or, which amounts to the same thing, a procedure to synchronize clocks in different points. Einstein then says that we are free to synchronize clocks in different points in such a way that the speed of light always turns out to be the same in opposite directions.
This raises an interesting question: by applying the Einstein clock adjustment procedure to sound signals, is it possible to make the speed of sound relative to an aircraft flying at subsonic speed the same in the “forward” and “backward” directions, too?
My answer is that, yes, technically that can be done, but it turns out that the Einstein clock adjustment procedure applied to sound is not a synchronization procedure. It therefore leaves us without any meaningful concept of simultaneity and, as a result, the concepts of one-way speed and of cause and effect applied to signals become meaningless, too.
To see this in greater detail, I’ve worked out the transformations between the coordinate systems S1 and S2 of two observers moving at subsonic speeds v1 and v2 relative to an undisturbed body of air S0 using the Einstein clock adjustment procedure described in my previous post, but applied to sound moving at the two-way speed of vs in S0, rather than to light signals.
Without going into details, suffice it to say that the way I have derived the transformation formulas is based on the known empirical facts concerning the two-way speed of sound in S0, S1 and S2 and the known behaviour of single clocks and measuring rods moving at subsonic speeds in S0. The result I’ve arrived at is that, in standard configuration - in other words if (0, 0) in S1 coincides with (0, 0) in S2 - for any pair of coordinates (x, t) in S1, the coordinates (x', t') in S2 are
(1)
(2)
where
and
What I find striking about this result is its similarity with the Lorentz transformation of special relativity, according to which
and
where
Of particular significance is the presence of the term
in (2), which corresponds to
in the Lorentz transformation, where it is responsible for the causality "paradoxes" that arise in special relativity if hypothetical signals moving at superluminal speeds are considered.
As equation (2) shows, very similar "paradoxes" result with supersonic signals if we apply the Einstein clock adjustment procedure to sound. For example, if we consider the case of v1 = 0 and imagine a plane flying at v2 through S0, we can arrange for the nose of the plane to be millions of years "in the past" compared to the tail from the point of view of a passenger travelling on the plane provided v2 is sufficiently close to the speed of sound. So, passengers at the tail of the plane could travel into the distant "past" in terms of their S2-coordinates just by sauntering over to the nose. It turns out that doing so requires the passengers to travel at supersonic speeds relative to S0. In fact the condition that signal speeds u in S0 must meet if a signal sent out from a point in S2 is to arrive at a different point in S2 "before it was sent" is of the same form as in special relativity:
Other odd effects result if we let these passengers saunter back to the tail of the plane: in terms of S2 coordinates, however fast they walk or run, they would take millions of years to get back to the tail of the plane while only ageing by a few seconds, making for extreme "time dilation" during their journey.
None of this is really paradoxical - the way we adjust our clocks cannot result in any true paradoxes - it is just utterly nonsensical. Just in what sense it is nonsensical, and what this means for the Einstein synchronization procedure applied to light signals, will require careful analysis and interpretation - in my next post.








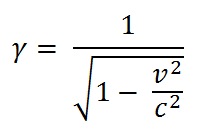



I know I should try harder to understand the deepest mysteries of the universe, but what do you do if the choice is between doing this and doing domestic chores? The latter of course because it’s a necessity. - Nonetheless: I'm deeply impressed by your knowledge and ability explaining your ideas to a wider public. And I wish I could follow and discuss all this with you.
ReplyDelete