So, what do Mansouri and Sexl mean when they say that "a theory maintaining absolute simultaneity is equivalent to special relativity"? Are they right? And what, if anything, does that tell us about the role of convention in Einstein's light speed principle?
First, let's see how Mansouri and Sexl approach the issue. They begin by assuming that Einstein's clock adjustment procedure has been applied in a first frame of reference Σ. The authors then consider a second frame S whose origin moves at v < c with respect to Σ, as measured with standard rods and clocks in Σ. They assume that the relationship between coordinates (X, T) in Σ and (x, t) in S is linear and they express that relationship in the following form:
t = aT + εx
(1)
x = b(X - vT)
It is striking that, rather than opting for a standard linear transformation in which t and x are represented in terms of T and X:
t = AT + BX
(2)
x = CT + DX
Mansouri and Sexl choose to present t as a function of T and x. (1) and (2) are equivalent in the sense that a, ε, b and v can be expressed in terms of A, B, C and D and vice versa. The reason why the authors use (1) rather than (2) is that the factors a, b, v and ε have special significance. As Mansouri and Sexl point out, a and b represent "the time dilatation and length contraction factors", which may depend on v and are a matter of empirical fact, while "arbitrary values of ε can be achieved" by choosing a suitable clock adjustment mechanism.
To see why b can be interpreted as a "length contraction" factor, consider the following diagram:
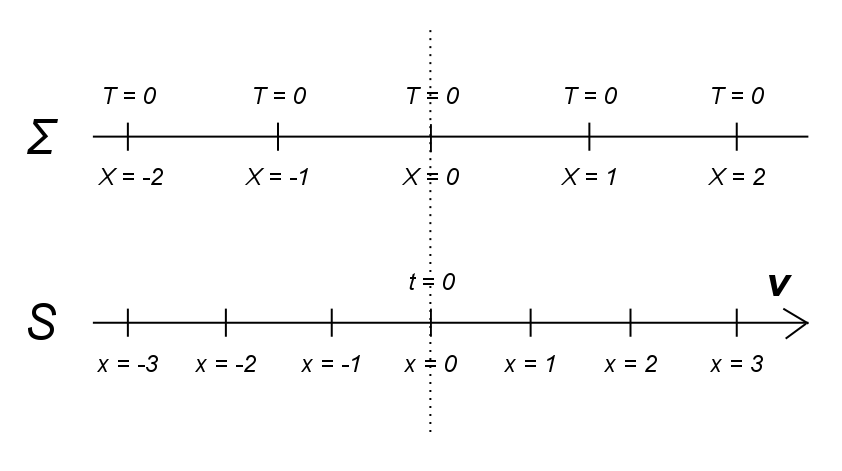Figure 1
In this diagram, clocks in Σ have been Einstein-adjusted, so in Σ time coordinates are well-defined in any location. In S, by contrast, distant clocks have not yet been adjusted, so we can only specify a time for a single clock. We choose that clock to be the one located at x = 0 and set it so that (x, t) = (0, 0) in S and (X, T) = (0, 0) in Σ coincide.
Now, it may be found empirically that any x differs from the X with which it coincides by a particular factor. Assuming that movement at v relative to Σ affects measuring rods at any location in S equally compared to identical measuring rods in Σ, this length contraction/dilation factor is the same for any pair of coinciding coordinates x, X in Figure 1 and also for any coinciding lengths l in S and L in Σ. Inserting T = 0 in (1), we obtain x = bX, so b is that length contraction/dilation factor.
To see that a is the time dilation factor, consider the following diagram, which shows the situation of Figure 1 after the Time T1 has passed in Σ:
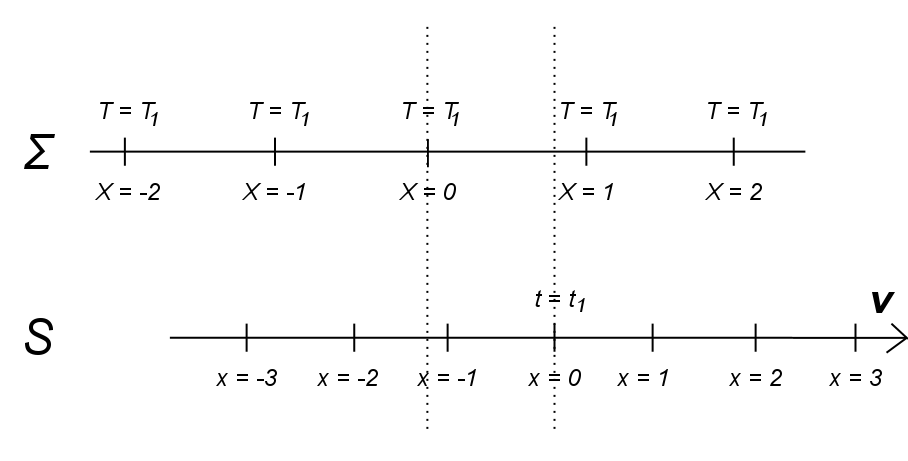Figure 2
It may be found empirically that t1 differs from T1 by a particular factor. Assuming that movement at v relative to Σ affects clocks equally at any location and time in S, this time contraction/dilation factor is the same for any single clock in S passing a series of clocks of identical construction in Σ. Inserting x = 0 in (1), we obtain t1 = aT1 , so a is that time contraction/dilation factor.
And that's all in the relationship between S coordinates and Σ coordinates that is a matter of empirical fact. How we set the time on clocks in S in locations other than x = 0 is a matter of choice, preference, decision-making, convention... and that choice is expressed mathematically in the value of ε, which may in fact be chosen to be a function of x as well as v. In terms of the factors occurring in (2) it can be expressed as ε = B/D, while b = D, v = -C/D and a = BC/D - A.
As Mansouri and Sexl point out, the value of ε in special relativity is -v/c2. This value can be called "relativity's conventionality factor". It was chosen by Einstein because it ensures that the one-way speed of light is the same for every observer in every frame of reference, which in turn ensures that the laws of physics take on a particularly simple form.
But what if a different value is chosen, say ε = 0 for any reference frame moving at any speed v relative to Σ? Mansouri and Sexl state that this particular case leads to a theory maintaining absolute simultaneity. What they mean by that is that, in the framework of this theory, two events that have the same time coordinate in a frame S moving at v relative to Σ also have the same time coordinate in any other frame S' moving at v' relative to Σ. In other words, if two events have coordinates (t1, x1) and (t2, x2) in S and (t1', x1') and (t2', x2') in S', then t1 = t2 if and only if t1' = t2'. This follows from ε = 0 in (1) by first transforming t1 and t2 into T1 and T2 in Σ and then T1 and T2 into t1' and t2' in S'.
Mansouri and Sexl add that a theory in which the conventionality factor is set to ε = 0 is "equivalent to special relativity" in the sense that if the outcome of an experiment can be predicted correctly using special relativity, then it can also be predicted correctly using a theory in which ε = 0, and vice versa. This is no doubt true because the conventionality factor merely expresses how we have chosen to adjust distant clocks and that does not in and of itself tell us anything about the world.
Nevertheless, Mansouri and Sexl dismiss the choice of ε = 0 as an "unsuitable" convention. Their reasons for this conclusion and the implications for the role of convention in the light speed principle will be the subject of my next post.
The article "A Test Theory of Special Relativity: I. Simultaneity and Clock Synchronization"
by Reza Mansouri and Roman U. Sexl, published in 1977, contains at
least two statements that are pertinent to my current investigation into
the role of convention in Einstein's light speed principle.
The
first is that "one of the most debated problems in special relativity
is the role of convention in the definition of simultaneity of distant
events and the related question of first-order experiments (first order
in v/c)" (p. 498).
"One
of the most debated problems in special relativity"! As is clear from
my last few posts, that's not exactly reflected in some recent textbooks
on special relativity purportedly focusing on conceptual issues.
Mansouri
and Sexl quickly make it clear that they believe convention plays an
important role in clock synchronization and thus in the definition of
simultaneity. They state, for example, that "Einstein's procedure to
synchronize clocks at different space points is but one of several
possible alternative conventions".
Mansouri
and Sexl are thus effectively saying that the synchronization of clocks
is a matter of convention. They do not give any particular reason for
this statement beyond listing a number of clock adjustment procedures
which they all label synchronization procedures.
And
that's the crux of the matter. I think it's important to be absolutely
clear about what exactly is conventional in Einstein's theory: it's the
choice of clock adjustment procedure. Anybody is free to adjust distant
clocks any way they like, and some such procedure may be adopted by a
whole community or even the whole world as the one to be applied by
convention. But, and this is a big but, not every clock adjustment
procedure is a synchronization procedure.
To
prove that point, it is sufficient to give examples of clock adjustment
procedures which are not synchronization procedures, and I have done
this in, for example, this and this
post. Drawing on those examples, I have argued that in general terms an
Einstein-like clock adjustment procedure using signals is a
synchronization procedure if and only if the signals used are emitted
and propagate in symmetrical conditions in all directions. And I have
concluded that on that basis Einstein's clock adjustment procedure is
not and cannot be a synchronization procedure.in all uniformly moving
frames of reference.
All
that may seem straightforward enough. But there is a possible objection
to my line of reasoning which I think I need to address in greater
detail than I have done.
The
objection broadly goes like this: "True, there may have been a time
when the idea of simultaneity was based on that of sending out signals
in symmetrical conditions, but that concept of simultaneity has become
untenable because it's emerged that it's impossible to distinguish
between frames of reference in which such symmetry pertains and frames
in which it doesn't. Therefore physicists have redefined
the concept and have agreed to call distant events with the same time
stamp according to Einstein-adjusted clocks "simultaneous". Even if that
definition hasn't filtered through into general usage, it's a technical
definition of the kind scientists use all the time to ensure their
concepts are precise and can be applied operationally. For example,
mathematicians talk about "groups" and "rings" in algebra in a very
precise technical sense, and they're perfectly free to do so even though
the concepts of a "group" or "ring" are used in very different ways in
non-mathematical contexts."
Indeed.
Absolutely. Physicists are free to do this. But then they shouldn't be
using the concept of "simultaneity (physics)" in contexts in which only
the symmetry-based concept of simultaneity makes sense. Just like
mathematicians shouldn't - and to the best of my knowledge generally
don't - use their concept of a "group (algebra)" to talk about group
dynamics in social situations, for example.
To
be more specific: I think the concept of simultaneity is closely linked
to concepts such as synchronization, symmetry, existence, signal,
speed, and cause and effect. This link is established in the way people
generally think, talk and write about these various concepts. It is thus
ingrained in the English language as currently constituted. Similar
considerations probably apply to many other languages in which similar
concepts exist.
I think the following statements exemplify some of the relationships between those concepts as currently constituted:
1)
Events in two places A and B are simultaneous if and only if
synchronized clocks located at A and B show the same time when the
events occur.
2)
Clocks in A and B can be synchronized by setting them to the same time
when identical signals emitted in opposite directions from the mid-point
M between A and B arrive at the clocks, provided the signals propagate
in symmetrical conditions.
3)
Signals sent from A to B cannot arrive in B at an earlier time than
when they were emitted as measured by synchronized clocks in A and B.
4)
If a signal emitted from A arrives in B at an earlier time than when it
was emitted, according to clocks positioned in A and B, then those
clocks aren't synchronized.
5)
A cause in a location A always precedes its effect at a distant
location B provided the clocks used to measure time in A and B are
synchronized.
6)
The one-way speed of a signal between A and B is the distance between A
and B divided by the time the signal needs to travel from A to B as
measured by synchronized clocks in A and B.
Some
of the meaning of "simultaneity", "synchronization", "symmetry",
"signal", "speed" and "cause and effect" is established in these
relationships.
It
is thus not possible to "redefine" one such concept and expect its
relationship with other, related concepts to be unaffected. For example,
I would hold that the concept of cause and effect relies on a
symmetry-based concept of simultaneity and becomes inapplicable in some
circumstances if the requirement of symmetry is given up.
And
this is exactly what happens if Einstein's clock adjustment procedure
is adopted: while we may not know whether light signals propagate
symmetrically in any particular uniformly moving frame of reference, we
do know that if they propagate symmetrically in a first frame then they
do not propagate symmetrically in other frames that move relative to the
first, at least not locally. The result is that the concept of cause
and effect, for example, becomes inapplicable in the context of special
relativity if superluminal speeds are involved.
Suggestions that superluminal speeds lead to cause and effect or the flow of time being "reversed", as they keep being made
in relation to recent neutrino experiments at CERN, are thus misguided:
they are the result of uncritically and unwittingly applying concepts
that rely on a symmetry-based concept of simultaneity to a theory in
which that concept has been abandoned.
After
this little digression, it's time to mention the second statement made
by Mansouri and Sexl that is pertinent to my investigations. This is the
"remarkable result", as the authors describe it, that "a theory maintaining absolute simultaneity is equivalent to special relativity" (Mansouri/Sexl's emphasis, p. 503).
My discussion of this statement will, however, have to wait until my next post.
Vesselin Petkov's Relativity and the Nature of Spacetime (2005) promises to specifically address "conceptual questions" relating to special relativity, such as "the physical meaning of the relativity of simultaneity" (p. 1, Petkov's emphasis), so this book should be right up my street.
As it turns out, it is anything but. The reason is that, far from probing the foundations of special relativity, Petkov takes them for granted. What is more, he takes a literal interpretation of those foundations for granted, no questions asked.
More specifically, of the three questions I have raised in previous posts:
- how decision-making contributes to the principle of the constancy of the speed of light;
- why it may be useful or advisable to adjust clocks in line with Einstein's procedure;
- and whether or in what sense Einstein's clock adjustment procedure can be regarded as a synchronization procedure and whether, therefore, it leads to meaningful statements about one-way speeds, simultaneous existence and causality
Petkov answers none. In fact, he doesn't even mention Einstein's clock adjustment procedure or the issue of clock synchronization, so in that sense he has even less to say about these issues than Leo Sartori in Understanding Relativity (1996), if that's possible.
How then does Petkov explain the principle of the constancy of the speed of light? He says it's a consequence of Galileo's principle of relativity, which according to him states that "by performing mechanical experiments, the uniform motion of a body cannot be detected" (p. 26). Petkov later makes it clear that by "motion" he means "absolute motion" relative to "some kind of medium" that pervades all of space (pp. 30-32).
Petkov seems to take the empirical finding that the two-way speed of light is always c for granted since he moves straight to the issue of the one-way speed of light. He argues that observers who "determine" or "see" or "observe" that the speed of light is not the same in every direction "would discover their absolute uniform motion", and since that's not possible according to the relativity principle they cannot observe any such thing (pp. 40-41).
What Petkov fails to realize, or to mention, is that in the first instance the constancy of the speed of light in every direction is not a matter that can be "determined" or "seen" or "observed" because before we can make such an observation we first need to adjust distant clocks. To do that, we need to decide on a clock adjustment procedure. We could, for example, try to adjust our clocks such that those clocks are synchronized, in other words such that equal time coordinates define a relationship of simultaneity.
As Einstein observed, two clocks may be synchronized by setting them to zero when a signal sent in all directions from the mid-point between the two clocks arrives there - provided the conditions of signal emission and propagation are symmetrical in all directions. Concepts such as one-way speed, simultaneous existence and causality are interwoven with and depend on this notion of simultaneity.
But, as Max Born suggested, it is difficult to be sure whether the conditions in which light or anything else propagates are symmetrical in every direction because we don't know the full list of parameters on which such symmetry might depend. I have proposed that local acceleration history might be one such parameter that is missing from current models, but this is just an idea at this stage, an idea which I will have to explore in much greater detail in the months and years to come.
Einstein adopted a different approach: he effectively proposed that we should dispense with the requirement of synchronization and instead adjust our clocks such that the laws of physics, in particular those of electrodynamics, take on a particularly simple form. Out of that, the elegant theory of special relativity was born. Elegant certainly, but with the drawback that the concepts of one-way speed, simultaneous existence and causality are no longer fully applicable in that theory.
There is thus more to special relativity than Petkov's formulation of Galileo's principle of relativity. In particular, special relativity is partly based on Einstein's choice of clock adjustment procedure with all its conceptual consequences. This issue is completely lost to Petkov. Instead, he takes Einstein's clock adjustment procedure and the idea that it represents a synchronization procedure for granted. Literally. For he concludes that according to relativity every event is simultaneous with every other in this world and that we therefore live in a block universe in which the flow of time is just an illusion - a typical example of the simultaneity syndrome in modern physics.
Over my last few blog entries, I have looked at the way in which three contemporary specialists on special relativity discuss the role of decision-making or convention in the principle of the constancy of c, in textbooks or monographs that set out to clarify the main conceptual issues relating to special relativity. What I have found is that neither Sartori (1996) nor Rindler (2001) nor Petkov (2005) even mention, let alone discuss, the issue of whether or in what sense Einstein's clock adjustment procedure is a synchronization procedure, and only Rindler suggests an answer to the question of why it may be useful or advisable to adopt Einstein's procedure.
I think the time has now come for me to turn my attention to some other texts in the literature which I hope and believe offer deeper answers to my questions. The first of these is an article published in 1977 by Reza Mansouri and Roman U. Sexl, followed finally by Kevin Brown's very important book, Reflections on Relativity (2010).
Reports that scientists at CERN have found neutrinos to travel faster than light do not necessarily mean that special relativity is wrong.
First, the difference to the speed of light is apparently very small, so this could easily be the result of errors in setting up the experiment, measuring relevant variables, synchronizing clocks... The author of the report on the experiment has said himself that "we are not claiming things, we want just to be helped by the community in understanding our crazy result".
Second, there are already a number of known "faster-than-light" phenomena which are not deemed to contradict relativity, and this may turn out to be just another one of those.
Third, I note that the reported result of the neutrino speed experiment chimes rather well with two of my findings relating to special relativity developed in this blog so far:
1) Faster-than-light signals would not involve any reversal of cause and effect and would not enable time travel into the past, according to a proper understanding of special relativity which avoids the trap of the "simultaneity syndrome" in modern physics.
2) The acceleration of macroscopic objects may be constrained by the fact that they contain electrically charged particles, which cannot be accelerated beyond the speed of light because light itself can be regarded as outwardly propagating disturbances in the electric fields of charged particles, as mentioned in this post.
For example, let there be an electron surrounded by or made up of a spherically symmetrical electric field, which can be visualized as a series of concentric spheres around the electron. If the electron is briefly accelerated, the distance between neighbouring spheres is reduced in the direction of acceleration and increased in the opposite direction as the information about the acceleration travels outwards. The disturbance of the electric field - an electromagnetic signal - is located at the boundary between the spheres that have been accelerated and those that haven't.
The law of light propagation could quite simply be that electromagnetic radiation emanating from an accelerated electron always traverses the same number of spheres as defined above in the same period of time as measured by Einstein-adjusted clocks in the system of the electron prior to acceleration.
According to this model, accelerating objects that contain electric charges also produce outwardly propagating field disturbances and are surrounded by "spheres" that move ever closer to each other in the direction of acceleration. The inability to accelerate charged particles up to or beyond the speed of light could then be a consequence of the fact that those spheres cannot be compressed to infinite density or beyond.
Particles that do not carry any electric charge, on the other hand, would not be constrained in the same way, though there may be other constraints regarding their acceleration.
The sphere model is a line of thought I intend to develop later, once I've reached the appropriate point in my understanding of special relativity as developed in this blog.
Five years after Leo Sartori's book Understanding Relativity was published, Wolfgang Rindler published his Relativity - Special, General, and Cosmological (2001). Like Sartori, Rindler says the emphasis throughout his book is on "understanding the concepts" underlying relativity. But does he give fuller answers than Sartori to the questions of
● how decision-making contributes to the principle of the constancy of the speed of light;
● why it may be useful or advisable to adjust clocks in line with Einstein's procedure;
● and whether or in what sense Einstein's clock adjustment procedure can be regarded as a synchronization procedure and whether, therefore, it leads to meaningful statements about one-way speeds, simultaneous existence and causality?
In a nutshell, he does, but it is not easy to distill answers to those questions from his presentation.
For a start, Rindler does not mention Einstein's clock adjustment procedure in the context of his explanation of the light speed principle. Instead, Rindler asserts that the existence of an invariant velocity follows from the relativity principle and the assumption of causal invariance. According to him, the only function of the light speed principle is thus "to fix the invariant velocity", and "Maxwell's theory and the ether-drift experiments clearly suggest that it should be c" (pp. 12, 15).
I'm going to examine the kind of empirical and theoretical arguments for the light speed principle put forward by Rindler and others in due course, in the months and years to come. Suffice it to say that Maxwell's theory and the idea that there is an invariant velocity both presuppose a concept of distant simultaneity, a fact which is acknowledged and addressed in Einstein's 1905 paper but not even mentioned in Rindler's book.
Curiously, however, Rindler's book contains a subsequent and quite disconnected section entitled "The coordinate lattice; Definitions of simultaneity" (pp. 41-43), which does discuss the issue of what constitutes a "satisfactory" clock synchronization procedure. It is this section which suggests some answers to my questions.
Rindler begins by making the same mistake as Sartori. He maintains that, in order to synchronize clocks, "it is sufficient to emit a single light signal from the origin, say at time t0: each lattice clock is set to read t0 + r/c as the signal passes it, where r is its distance from the origin". Rindler thus uses the one-way speed of light to synchronize clocks when in fact a clock synchronization procedure must already be in place for that speed to be well-defined, as recognized by Einstein in his 1905 paper.
But then Rindler asks what actually makes for a satisfactory clock synchronization procedure, and some of his answers are instructive. "In particular," Rindler says, "the time coordinate t can be chosen so that the mathematical expression of the physical laws reflects their inherent symmetries."
Rindler makes three important points in this key sentence: first, as far as physicists are concerned, time coordinates are a matter of choice; second, that choice should be guided by the effect it has on the mathematical form of physical laws, in other words: whether or not such time coordinates define a relationship of simultaneity is quite irrelevant; third, the desired effect is for the "inherent symmetries" of physical laws to be preserved.
Rindler doesn't elaborate much on the last point, but he suggests that a situation in which a gun shoots bullets faster in one direction than another because of the way we have chosen our time coordinates should be avoided. At first sight this requirement may seem plausible enough. Galileo and Newton would no doubt have agreed. But then, they didn't know about high-speed particle experiments which show that it becomes ever more difficult to accelerate particles as they approach the speed of light. Today we know that a bullet fired in the forward direction by a gun moving at close to c through the laboratory moves more slowly away from that gun than a bullet fired by the same gun in the backward direction - as seen from the laboratory using Einstein-adjusted clocks, that is.
So why should time coordinates in the system of the gun be adjusted such that in that system the bullets move away from the gun at equal speeds in every direction? Rindler doesn't say explicitly, but the idea seems to be that if we do so the laws of physics take on a particularly simple, symmetric form in all uniformly moving frames of reference, just as they do in Newton's theory and in the "ether" frame of Maxwell's theory. The result is that, in Rindler's words, in special relativity every uniformly moving frame of reference is "as good as absolute space" in Newton's theory and also "as good as Maxwell's ether frame".
In a sense then, special relativity is a conservative enterprise: it defines time coordinates, or adjusts clocks, in such a way that the laws of physics remain symmetrical in different directions just as in Newton's and Maxwell's theories of old - despite subsequent empirical findings suggesting that the phenomena themselves lack such symmetry.
The conservatism of special relativity is neatly encapsulated in a formula chosen by Rindler to describe how light propagates. "According to Einstein's second axiom, light in every inertial frame behaves like light in Maxwell's ether," Rindler says on p. 38 (his emphasis). It appears that the ether model has not been abandoned in modern physics, after all, but has been generalized to every inertial frame of reference!
There is nothing wrong with a conservative approach to physics as long as there are good reasons for it. Clearly, physicists have decided that they prefer to work with symmetrical laws, to which they have been used for centuries. Even if they were prepared to admit asymmetrical laws, there would still be the small matter of determining in which frames of reference, if any, bullets or light propagate in symmetrical conditions in every direction so that Einstein's clock adjustment procedure can be used to synchronize clocks in those frames, as discussed in a previous post.
But the conservatism of special relativity comes at a price. By clinging on to symmetrical laws through a suitable choice of time coordinates, special relativity dispenses with the requirement that clocks should be synchronized and thus throws concepts such as one-way speed, simultaneous existence and causality into disarray, as illustrated by the "simultaneity syndrome" in modern physics discussed in this post.
Rindler does not seem to be aware of this problem as he refers to a clock adjustment procedure based on the light speed principle as a way of "synchronizing clocks", without any qualification, and a few pages later he promptly falls victim to the "simultaneity syndrome". In summary, then, Rindler gives answers to the first two questions set out at the start of this post but not to the third.
In my next post I will examine whether a book wholly devoted to "the meaning of spacetime", Vesselin Petkov's Relativity and the Nature of Spacetime (2005), gives a more satisfactory explanation of clock adjustment and synchronization in special relativity.
