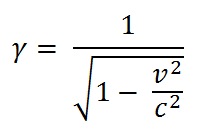According to the principle of the constancy of the speed of light in SR, if an observer chases after a flash of light, the light will keep moving away from the observer at the universal speed c no matter how much the observer speeds up. Likewise, if an observer runs into a flash of light, the light will keep moving towards the observer at c no matter how much the observer speeds up.
As I mentioned in a previous post, another consequence of the constancy of c is the possibility of causality paradoxes if hypothetical superluminal signals are considered. But at low speeds, too, there are some surprising effects. For example, if two observers A and B at rest relative to each other at opposite ends of the observable universe started to walk in the same direction A--> B--> at the same time, then, in accordance with the transformations of SR, A would suddenly have to consider that B set out 300 years earlier than A and is now long dead. If both stopped after a few metres, however, B would promptly come back to life as far as A is concerned since A would now consider that A and B set out at the same time, after all, and also stopped at the same time.
All this strangeness is at least partly the making of physicists because, as explained in previous posts, the notions of "simultaneity" and "one-way speed" as defined in SR crucially depend on Einstein's choice of clock adjustment procedure. It is now time to look at the literature on SR to see how physicists have justified such a clock adjustment procedure, and how they have defended the idea that it represents a synchronization procedure that may serve to define simultaneity and one-way speed.
Let me begin with a little survey of the texts I would like to examine. The first two are Albert Einstein's famous 1905 article "On the Electrodynamics of Moving Bodies" and his subsequent account of the main features of SR intended for a wider audience, first published in 1916. In my opinion, these two publications are much clearer regarding the foundations of special relativity than many other texts published on the subject since. In particular, Einstein is perfectly lucid on the role of convention, definition or stipulation in his theory. On the other hand, there is very little in these texts to motivate or justify his clock adjustment procedure, let alone the idea that it may serve as a synchronization procedure.
This is perhaps unsurprising since, as far as I know, Einstein was addressing an audience whose main concern was to reconcile recent experimental results with the erroneous idea of an essentially static, all-pervasive medium for light, or "ether". He was not writing for future generations of students of physics who had never had any reason to believe in such an "ether" in the first place and were much more interested in the issue of meaningful synchronization procedures.
This is where modern textbooks and other publications focusing on the foundations of special relativity come in. Two which I would like to consider are an online article by Allen Janis wholly dedicated to the issue of the "Conventionality of Simultaneity" in SR, and a 1977 article by Reza Mansouri and Roman U. Sexl on "A Test Theory of Special Relativity: I. Simultaneity and Clock Synchronization". In addition, I have identified four books which are of particular interest to me because of their explicit emphasis on the concepts underlying SR: Leo Sartori's Understanding Relativity (1996); Wolfgang Rindler's Relativity: Special, General, Cosmological (2001); Vesselin Petkov's Relativity and the Nature of Spacetime (2005); and above all Kevin Brown's Reflections on Relativity (2010).
Kevin Brown's book is particularly relevant to my project because it explicitly addresses some of the very same issues I am grappling with in this blog. What is more, it gives a clear, coherent and erudite account of the foundations of SR unrivalled by any of the other texts I have mentioned. If there is hope for my understanding of the principle of the constancy of c, it lies in Kevin Brown's book!
But first things first, so let me start with Brown's illustrious precursor, Albert Einstein - in my next post.
This blog is motivated by my desire to understand the special theory of relativity, in particular the principle of the constancy of the speed of light for every observer. How did physicists come to accept it? Is it based on convention, theory or observation? Are there any alternative conventions or theories that are compatible with observation and experiment?
Tuesday, 7 December 2010
Sunday, 7 November 2010
More on sound, light and time
So, in what sense does the application of the Einstein clock adjustment procedure to sound signals lead to nonsensical results, and why?
As we have seen, it leads for example to the result that walking speeds become infinitely fast in some frames of reference, and that, by speeding up a little bit more, it becomes possible to walk into the past in such frames. The concepts of one-way speed and causality thus break down. In purely mathematical terms, people would even be able to cause serious causality paradoxes by walking into the past and then turning round and arriving back home before they left. Of course, this is not actually possible because it would be physically impossible to move back at a sufficiently high speed - ultimately because the mathematical "plane of simultaneity" defined by such a clock adjustment procedure is not actually a plane of simultaneity at all. The concept of simultaneity thus breaks down.
It therefore seems that the Einstein synchronization procedure cannot be applied to sound signals. But what about the idea that synchronization is just a matter of definition? In other words, prior to deciding on a synchronization procedure, how can we know that, from the point of view of an observer moving relative to a body of air, the one-way speed of sound is not equal in different directions?
First, we can use a limited concept of one-way speed that is independent of any synchronization procedure: the one-way speed of a first signal sent out from A is higher, equal to or lower than that of a second signal sent out from A at the same time if the first signal arrives in B before, at the same time as or after the second, respectively. Clocks in A and B do not need to be synchronized to make such observations. The concept of one-way speed in a single direction is thus well-defined in comparative terms - lower, equal or higher - regardless of any synchronization procedure.
Now consider an observer A who is stationary with respect to a body of air. This observer will find empirically that different signals sent out from A, including sound signals, exhibit the same relative one-way speeds as defined above regardless of the direction in which they are sent out. An observer B moving relative to the same stationary body of air, however, will find that sound signals sent out from B in the "forward" direction travel more slowly compared to the same range of other signals sent out from B, while sound signals sent out in the "backward" direction travel faster compared to the same range of other signals. The second observer thus has good reasons to conclude on empirical grounds that the one-way speed of sound is not equal in the forward and backward directions even prior to defining any synchronization procedure.
But there is more. Our theoretical knowledge of how sound waves propagate, too, tells us that, for an observer travelling relative to a body of air, the one-way speeds of sound in the forward and backward directions cannot be equal. We know, for example, that sound consists of outwardly propagating vibrations of air molecules. This means that, for an observer who is stationary relative to a body of air, the conditions in which sound propagates are symmetrical in all directions, while for an observer moving relative to a body of air the conditions in which sound propagates are not symmetrical. We can therefore expect the one-way speed of sound to be equal in different directions for the first observer and unequal for the second.
And there is even more. For any signal, if we believe, assume or stipulate that the conditions in which it propagates are symmetrical for a given observer, then it is difficult to see how they can also be symmetrical for a second observer who is moving relative to the first. This seems fundamental to me and it goes to the heart of my difficulties in getting to grips with the special theory of relativity.
I have no particular problem with the idea that acceleration may lead to the slowing down of clocks or even the contraction of measuring rods. The empirical finding that the two-way speed of light is always measured as c, if indeed there is such an empirical finding, is somewhat surprising but may be explicable precisely as a result of the effects of acceleration on clocks and measuring rods - in fact, if there are such effects, we may choose to correct for them by adjusting the rate at which clocks that have undergone acceleration tick, resulting in the two-way speed not always being measured as c.
But what I cannot yet fathom is on what grounds generations of physicists have seen fit to declare that, if the conditions in which light propagates are deemed to be symmetrical relative to a source of light, the one-way speed of light is deemed to be the same in all directions even for an observer who is moving relative to that source of light. Or why they would want to adjust clocks in such a way that it is made to be the same in all directions for such an observer.
What I have endeavoured to show thus far is that, while of course physicists are free to adjust clocks in this way, they are not free to declare that such a clock adjustment procedure is a synchronization procedure. And that if it isn't the concepts of simultaneity, one-way speed and causality may be undermined. Ultimately, then, it may turn out that special relativity is certainly a usable theory in that it successfully predicts the outcome of experiments, but that it relies on a clock adjustment procedure which is not a synchronization procedure and that therefore the concepts of one-way speed, simultaneity and causality have limited applicability in the framework of that theory.
I think it is now time for a few propositions relating to the role played by definition or stipulation in the principle of the constancy of the speed of light for every observer in the special theory of relativity.
P1: The constancy of the two-way speed of light in every coordinate system in which the laws of mechanics hold is an empirical matter once the rate at which clocks in different such coordinate systems tick has been set.
P2: The constancy of the one-way speed of light in every direction in every coordinate system in which the laws of mechanics hold is an empirical matter once a synchronization procedure for clocks in different locations in different such coordinate systems has been decided on.
P3: Not every clock adjustment procedure is a clock synchronization procedure.
P4: A clock adjustment procedure resulting in clock settings under which a signal sent from a location A may arrive in a location B "before it was sent" is not a synchronization procedure.
P5: A clock adjustment procedure that relies on sending a signal from location A to B and back and sets the signal arrival time in B to be in the middle between the signal sending and arrival times in A is a synchronization procedure only if the conditions in which the signal propagates are symmetrical in both directions.
So, is the Einstein clock adjustment procedure using light signals a synchronization procedure? On the face of it it is difficult to see how it can be, but once again, the answer depends on a number of empirical and theoretical issues which I have yet to look into in any detail over the months and years to come.
Before I embark on this quest, I think it's high time I started reviewing what the physics literature has to say on the role of definition or stipulation in the principle of the constancy of the speed of light for every observer - in my next blog post.
As we have seen, it leads for example to the result that walking speeds become infinitely fast in some frames of reference, and that, by speeding up a little bit more, it becomes possible to walk into the past in such frames. The concepts of one-way speed and causality thus break down. In purely mathematical terms, people would even be able to cause serious causality paradoxes by walking into the past and then turning round and arriving back home before they left. Of course, this is not actually possible because it would be physically impossible to move back at a sufficiently high speed - ultimately because the mathematical "plane of simultaneity" defined by such a clock adjustment procedure is not actually a plane of simultaneity at all. The concept of simultaneity thus breaks down.
It therefore seems that the Einstein synchronization procedure cannot be applied to sound signals. But what about the idea that synchronization is just a matter of definition? In other words, prior to deciding on a synchronization procedure, how can we know that, from the point of view of an observer moving relative to a body of air, the one-way speed of sound is not equal in different directions?
First, we can use a limited concept of one-way speed that is independent of any synchronization procedure: the one-way speed of a first signal sent out from A is higher, equal to or lower than that of a second signal sent out from A at the same time if the first signal arrives in B before, at the same time as or after the second, respectively. Clocks in A and B do not need to be synchronized to make such observations. The concept of one-way speed in a single direction is thus well-defined in comparative terms - lower, equal or higher - regardless of any synchronization procedure.
Now consider an observer A who is stationary with respect to a body of air. This observer will find empirically that different signals sent out from A, including sound signals, exhibit the same relative one-way speeds as defined above regardless of the direction in which they are sent out. An observer B moving relative to the same stationary body of air, however, will find that sound signals sent out from B in the "forward" direction travel more slowly compared to the same range of other signals sent out from B, while sound signals sent out in the "backward" direction travel faster compared to the same range of other signals. The second observer thus has good reasons to conclude on empirical grounds that the one-way speed of sound is not equal in the forward and backward directions even prior to defining any synchronization procedure.
But there is more. Our theoretical knowledge of how sound waves propagate, too, tells us that, for an observer travelling relative to a body of air, the one-way speeds of sound in the forward and backward directions cannot be equal. We know, for example, that sound consists of outwardly propagating vibrations of air molecules. This means that, for an observer who is stationary relative to a body of air, the conditions in which sound propagates are symmetrical in all directions, while for an observer moving relative to a body of air the conditions in which sound propagates are not symmetrical. We can therefore expect the one-way speed of sound to be equal in different directions for the first observer and unequal for the second.
And there is even more. For any signal, if we believe, assume or stipulate that the conditions in which it propagates are symmetrical for a given observer, then it is difficult to see how they can also be symmetrical for a second observer who is moving relative to the first. This seems fundamental to me and it goes to the heart of my difficulties in getting to grips with the special theory of relativity.
I have no particular problem with the idea that acceleration may lead to the slowing down of clocks or even the contraction of measuring rods. The empirical finding that the two-way speed of light is always measured as c, if indeed there is such an empirical finding, is somewhat surprising but may be explicable precisely as a result of the effects of acceleration on clocks and measuring rods - in fact, if there are such effects, we may choose to correct for them by adjusting the rate at which clocks that have undergone acceleration tick, resulting in the two-way speed not always being measured as c.
But what I cannot yet fathom is on what grounds generations of physicists have seen fit to declare that, if the conditions in which light propagates are deemed to be symmetrical relative to a source of light, the one-way speed of light is deemed to be the same in all directions even for an observer who is moving relative to that source of light. Or why they would want to adjust clocks in such a way that it is made to be the same in all directions for such an observer.
What I have endeavoured to show thus far is that, while of course physicists are free to adjust clocks in this way, they are not free to declare that such a clock adjustment procedure is a synchronization procedure. And that if it isn't the concepts of simultaneity, one-way speed and causality may be undermined. Ultimately, then, it may turn out that special relativity is certainly a usable theory in that it successfully predicts the outcome of experiments, but that it relies on a clock adjustment procedure which is not a synchronization procedure and that therefore the concepts of one-way speed, simultaneity and causality have limited applicability in the framework of that theory.
I think it is now time for a few propositions relating to the role played by definition or stipulation in the principle of the constancy of the speed of light for every observer in the special theory of relativity.
P1: The constancy of the two-way speed of light in every coordinate system in which the laws of mechanics hold is an empirical matter once the rate at which clocks in different such coordinate systems tick has been set.
P2: The constancy of the one-way speed of light in every direction in every coordinate system in which the laws of mechanics hold is an empirical matter once a synchronization procedure for clocks in different locations in different such coordinate systems has been decided on.
P3: Not every clock adjustment procedure is a clock synchronization procedure.
P4: A clock adjustment procedure resulting in clock settings under which a signal sent from a location A may arrive in a location B "before it was sent" is not a synchronization procedure.
P5: A clock adjustment procedure that relies on sending a signal from location A to B and back and sets the signal arrival time in B to be in the middle between the signal sending and arrival times in A is a synchronization procedure only if the conditions in which the signal propagates are symmetrical in both directions.
So, is the Einstein clock adjustment procedure using light signals a synchronization procedure? On the face of it it is difficult to see how it can be, but once again, the answer depends on a number of empirical and theoretical issues which I have yet to look into in any detail over the months and years to come.
Before I embark on this quest, I think it's high time I started reviewing what the physics literature has to say on the role of definition or stipulation in the principle of the constancy of the speed of light for every observer - in my next blog post.
Tuesday, 21 September 2010
How to use sound to do things with time
I know it’s been a long time, but what do you do if the choice is between exploring the deepest mysteries of the universe and doing domestic chores? The latter of course because it’s a necessity.
So, once again, to what extent is the idea that the speed of light is the same for every observer based on convention, stipulation or definition rather than theory or empirical fact? As we’ve seen, according to Einstein the constancy of c is partly a matter of definition. In his 1905 article "On the Electrodynamics of Moving Bodies", he said we are free to define simultaneity in different points in such a way that the speed of light is always the same in opposite directions.
At first sight, this seems an astonishing thing to say in view of the empirical fact that, if a source of light moves relative to the laboratory near the speed of light, then light seems to move more slowly away from that source in the “forward” direction than it does in the “backward” direction, just like the sound caused by an aircraft flying near the speed of sound moves more slowly away from the nose of the aircraft than it does from the tail of the aircraft.
However, the “empirical fact” just cited depends on measurements of the one-way speed of light in the “forward” and the “backward” direction. Einstein correctly observes that, in order to measure such one-way speeds, we first need a definition of simultaneity in different points or, which amounts to the same thing, a procedure to synchronize clocks in different points. Einstein then says that we are free to synchronize clocks in different points in such a way that the speed of light always turns out to be the same in opposite directions.
This raises an interesting question: by applying the Einstein clock adjustment procedure to sound signals, is it possible to make the speed of sound relative to an aircraft flying at subsonic speed the same in the “forward” and “backward” directions, too?
My answer is that, yes, technically that can be done, but it turns out that the Einstein clock adjustment procedure applied to sound is not a synchronization procedure. It therefore leaves us without any meaningful concept of simultaneity and, as a result, the concepts of one-way speed and of cause and effect applied to signals become meaningless, too.
To see this in greater detail, I’ve worked out the transformations between the coordinate systems S1 and S2 of two observers moving at subsonic speeds v1 and v2 relative to an undisturbed body of air S0 using the Einstein clock adjustment procedure described in my previous post, but applied to sound moving at the two-way speed of vs in S0, rather than to light signals.
Without going into details, suffice it to say that the way I have derived the transformation formulas is based on the known empirical facts concerning the two-way speed of sound in S0, S1 and S2 and the known behaviour of single clocks and measuring rods moving at subsonic speeds in S0. The result I’ve arrived at is that, in standard configuration - in other words if (0, 0) in S1 coincides with (0, 0) in S2 - for any pair of coordinates (x, t) in S1, the coordinates (x', t') in S2 are
(1)
(2)
where
and
What I find striking about this result is its similarity with the Lorentz transformation of special relativity, according to which
and
where
Of particular significance is the presence of the term
in (2), which corresponds to
in the Lorentz transformation, where it is responsible for the causality "paradoxes" that arise in special relativity if hypothetical signals moving at superluminal speeds are considered.
As equation (2) shows, very similar "paradoxes" result with supersonic signals if we apply the Einstein clock adjustment procedure to sound. For example, if we consider the case of v1 = 0 and imagine a plane flying at v2 through S0, we can arrange for the nose of the plane to be millions of years "in the past" compared to the tail from the point of view of a passenger travelling on the plane provided v2 is sufficiently close to the speed of sound. So, passengers at the tail of the plane could travel into the distant "past" in terms of their S2-coordinates just by sauntering over to the nose. It turns out that doing so requires the passengers to travel at supersonic speeds relative to S0. In fact the condition that signal speeds u in S0 must meet if a signal sent out from a point in S2 is to arrive at a different point in S2 "before it was sent" is of the same form as in special relativity:
Other odd effects result if we let these passengers saunter back to the tail of the plane: in terms of S2 coordinates, however fast they walk or run, they would take millions of years to get back to the tail of the plane while only ageing by a few seconds, making for extreme "time dilation" during their journey.
None of this is really paradoxical - the way we adjust our clocks cannot result in any true paradoxes - it is just utterly nonsensical. Just in what sense it is nonsensical, and what this means for the Einstein synchronization procedure applied to light signals, will require careful analysis and interpretation - in my next post.
So, once again, to what extent is the idea that the speed of light is the same for every observer based on convention, stipulation or definition rather than theory or empirical fact? As we’ve seen, according to Einstein the constancy of c is partly a matter of definition. In his 1905 article "On the Electrodynamics of Moving Bodies", he said we are free to define simultaneity in different points in such a way that the speed of light is always the same in opposite directions.
At first sight, this seems an astonishing thing to say in view of the empirical fact that, if a source of light moves relative to the laboratory near the speed of light, then light seems to move more slowly away from that source in the “forward” direction than it does in the “backward” direction, just like the sound caused by an aircraft flying near the speed of sound moves more slowly away from the nose of the aircraft than it does from the tail of the aircraft.
However, the “empirical fact” just cited depends on measurements of the one-way speed of light in the “forward” and the “backward” direction. Einstein correctly observes that, in order to measure such one-way speeds, we first need a definition of simultaneity in different points or, which amounts to the same thing, a procedure to synchronize clocks in different points. Einstein then says that we are free to synchronize clocks in different points in such a way that the speed of light always turns out to be the same in opposite directions.
This raises an interesting question: by applying the Einstein clock adjustment procedure to sound signals, is it possible to make the speed of sound relative to an aircraft flying at subsonic speed the same in the “forward” and “backward” directions, too?
My answer is that, yes, technically that can be done, but it turns out that the Einstein clock adjustment procedure applied to sound is not a synchronization procedure. It therefore leaves us without any meaningful concept of simultaneity and, as a result, the concepts of one-way speed and of cause and effect applied to signals become meaningless, too.
To see this in greater detail, I’ve worked out the transformations between the coordinate systems S1 and S2 of two observers moving at subsonic speeds v1 and v2 relative to an undisturbed body of air S0 using the Einstein clock adjustment procedure described in my previous post, but applied to sound moving at the two-way speed of vs in S0, rather than to light signals.
Without going into details, suffice it to say that the way I have derived the transformation formulas is based on the known empirical facts concerning the two-way speed of sound in S0, S1 and S2 and the known behaviour of single clocks and measuring rods moving at subsonic speeds in S0. The result I’ve arrived at is that, in standard configuration - in other words if (0, 0) in S1 coincides with (0, 0) in S2 - for any pair of coordinates (x, t) in S1, the coordinates (x', t') in S2 are
(1)
(2)
where
and
What I find striking about this result is its similarity with the Lorentz transformation of special relativity, according to which
and
where
Of particular significance is the presence of the term
in (2), which corresponds to
in the Lorentz transformation, where it is responsible for the causality "paradoxes" that arise in special relativity if hypothetical signals moving at superluminal speeds are considered.
As equation (2) shows, very similar "paradoxes" result with supersonic signals if we apply the Einstein clock adjustment procedure to sound. For example, if we consider the case of v1 = 0 and imagine a plane flying at v2 through S0, we can arrange for the nose of the plane to be millions of years "in the past" compared to the tail from the point of view of a passenger travelling on the plane provided v2 is sufficiently close to the speed of sound. So, passengers at the tail of the plane could travel into the distant "past" in terms of their S2-coordinates just by sauntering over to the nose. It turns out that doing so requires the passengers to travel at supersonic speeds relative to S0. In fact the condition that signal speeds u in S0 must meet if a signal sent out from a point in S2 is to arrive at a different point in S2 "before it was sent" is of the same form as in special relativity:
Other odd effects result if we let these passengers saunter back to the tail of the plane: in terms of S2 coordinates, however fast they walk or run, they would take millions of years to get back to the tail of the plane while only ageing by a few seconds, making for extreme "time dilation" during their journey.
None of this is really paradoxical - the way we adjust our clocks cannot result in any true paradoxes - it is just utterly nonsensical. Just in what sense it is nonsensical, and what this means for the Einstein synchronization procedure applied to light signals, will require careful analysis and interpretation - in my next post.
Wednesday, 23 June 2010
The role of convention
So, what exactly is the role of stipulation, or convention, or definition, in the claim that the speed of light is always the same for every observer? Determining the average speed – or two-way speed - of a light signal moving in a straight line from A to B and back is clearly an empirical matter: all that is required is a single clock in A and the ability to determine the distance between A and B.
But what about the one-way speed, first from A to B and then from B to A? Is it necessarily the same on both legs of the journey? The question is relevant since, in some respects at least, light behaves like a wave, and the one-way speed between a wave and its source depends on the direction of travel of the wave if the source is in uniform motion relative to the medium in which the wave is travelling. That's a matter of empirical fact. Or is it?
In his 1905 article "On the Electrodynamics of Moving Bodies", Einstein argued that, in any coordinate system in which Newton's laws of mechanics hold, the question of whether or not the speed of light varies depending on the direction in which it travels is a matter of stipulation or definition rather than empirical fact.
Here's the relevant passage (p. 894):
'…so far we have only defined an "A time" [time at location A in a coordinate system in which Newton's laws of mechanics hold] and a "B time" [time at location B in the same coordinate system], but no "time" that is common to A and B. The latter time can now be defined by stipulating by definition that the time it takes for light to travel from A to B is the same as the time it takes for it to travel from B to A. For, let a ray of light leave A at "A time" tA in the direction of B, let it be reflected in B at "B time" tB in the direction of A and let it arrive back in A at "A time" t'A. The two clocks are defined to be synchronous if
tB – tA = t'A – tB. … '
In modern parlance, Einstein takes the view here that simultaneity is a matter of convention, and that we are free to define simultaneity by means of the Einstein synchronization procedure using light signals as outlined in the quote above. As a result of this definition, the one-way speed of light from A to B always turns out to be the same as from B to A. In this view, then, the equality of the speed of light in opposite directions in any coordinate system in which Newton's laws of mechanics hold is a matter of convention, too.
Do I agree with this conclusion? My provisional answer is "no", for three reasons:
1) It is true that it seems impossible to fully establish or even define the one-way speed of any signal without first defining simultaneity in different locations. However, certain findings about the one-way speeds of different signals, such as whether or not they are equal to or lower or higher than each other, can be obtained through experiment and observation without recourse to any definition of simultaneity in different locations. In conjunction with theories about how those signals propagate, which may also be based on experiment and observation, those findings may impose certain conditions on how simultaneity in different locations can be defined if what is being defined is to deserve the name of simultaneity.
2) The very notion of simultaneity implies a condition which any operational definition of simultaneity must meet if, again, what is being defined is to deserve the name of simultaneity, namely: if clocks in A and B are synchronized under the definition in question and if a signal that is sent from A at the time t1 arrives in B at the time t2, then t2 must be later than t1, i.e. t2 > t1.
3) On the basis of 1) and 2), I will show that applying the Einstein synchronization procedure to, for example, sound signals propagating through air does not yield a meaningful definition of simultaneity.
All of these points will be developed in greater detail in subsequent posts, in which I will also review what the physics texts mentioned in my first blog entry have to say about the issue. But even then I may not be in a position to say whether or not applying the Einstein synchronization procedure to light signals yields a meaningful definition of simultaneity. This is precisely because points 1) to 3) suggest that the answer depends on key theoretical and empirical findings relating to electromagnetic radiation, so ultimately I may well have to defer my final verdict until I have had a chance to review those. Whatever happens, I'm going to keep you posted.
But what about the one-way speed, first from A to B and then from B to A? Is it necessarily the same on both legs of the journey? The question is relevant since, in some respects at least, light behaves like a wave, and the one-way speed between a wave and its source depends on the direction of travel of the wave if the source is in uniform motion relative to the medium in which the wave is travelling. That's a matter of empirical fact. Or is it?
In his 1905 article "On the Electrodynamics of Moving Bodies", Einstein argued that, in any coordinate system in which Newton's laws of mechanics hold, the question of whether or not the speed of light varies depending on the direction in which it travels is a matter of stipulation or definition rather than empirical fact.
Here's the relevant passage (p. 894):
'…so far we have only defined an "A time" [time at location A in a coordinate system in which Newton's laws of mechanics hold] and a "B time" [time at location B in the same coordinate system], but no "time" that is common to A and B. The latter time can now be defined by stipulating by definition that the time it takes for light to travel from A to B is the same as the time it takes for it to travel from B to A. For, let a ray of light leave A at "A time" tA in the direction of B, let it be reflected in B at "B time" tB in the direction of A and let it arrive back in A at "A time" t'A. The two clocks are defined to be synchronous if
tB – tA = t'A – tB. … '
In modern parlance, Einstein takes the view here that simultaneity is a matter of convention, and that we are free to define simultaneity by means of the Einstein synchronization procedure using light signals as outlined in the quote above. As a result of this definition, the one-way speed of light from A to B always turns out to be the same as from B to A. In this view, then, the equality of the speed of light in opposite directions in any coordinate system in which Newton's laws of mechanics hold is a matter of convention, too.
Do I agree with this conclusion? My provisional answer is "no", for three reasons:
1) It is true that it seems impossible to fully establish or even define the one-way speed of any signal without first defining simultaneity in different locations. However, certain findings about the one-way speeds of different signals, such as whether or not they are equal to or lower or higher than each other, can be obtained through experiment and observation without recourse to any definition of simultaneity in different locations. In conjunction with theories about how those signals propagate, which may also be based on experiment and observation, those findings may impose certain conditions on how simultaneity in different locations can be defined if what is being defined is to deserve the name of simultaneity.
2) The very notion of simultaneity implies a condition which any operational definition of simultaneity must meet if, again, what is being defined is to deserve the name of simultaneity, namely: if clocks in A and B are synchronized under the definition in question and if a signal that is sent from A at the time t1 arrives in B at the time t2, then t2 must be later than t1, i.e. t2 > t1.
3) On the basis of 1) and 2), I will show that applying the Einstein synchronization procedure to, for example, sound signals propagating through air does not yield a meaningful definition of simultaneity.
All of these points will be developed in greater detail in subsequent posts, in which I will also review what the physics texts mentioned in my first blog entry have to say about the issue. But even then I may not be in a position to say whether or not applying the Einstein synchronization procedure to light signals yields a meaningful definition of simultaneity. This is precisely because points 1) to 3) suggest that the answer depends on key theoretical and empirical findings relating to electromagnetic radiation, so ultimately I may well have to defer my final verdict until I have had a chance to review those. Whatever happens, I'm going to keep you posted.
Subscribe to:
Comments (Atom)