Coulomb's law expresses the force between two charges q1 and q2 that are stationary in an inertial frame of reference Σ as a function of the distance r between them:
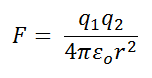
(Equation 1)
Can this equation be generalized to the case of two charges q1 and q2 which are stationary relative to each other but which are travelling at v through an inertial frame of reference Σ in which light propagates in symmetrical conditions and clocks have been Einstein-adjusted?
What form does Coulomb's law take in that case, and can the shape of that law be explained in terms of a simple model of how electric field disturbances propagate, without invoking length contraction, time dilation or magnetism?
Recall that in my sphere model of electricity, as discussed here, charges that are stationary in Σ are deemed to be surrounded by concentric electrical spheres with a particular sphere density λΣ = nΣ /r for a line of length r that starts in the origin.
(Figure 1)
When the charge is locally accelerated to a speed v in Σ and then continues to move at that speed, the information about the acceleration spreads through the spheres at the speed c, leading to the following situation after a time t has passed:
(Figure 2)
I will now consider the case of two charges q1 and q2 moving at v through Σ and separated by the distance r. Let n1 be the number of spheres surrounding q1 that cut through r ; n2 the number of spheres surrounding q2 that cut through r ; and β the angle at which the spheres that surround q1 and q2 cut through r :

(Figure 3)
(Figure 3)
The fact that the two angles marked β are the same can be seen by prolonging the line P2P3 in Figure 2 downwards until it meets the circle on which P3 lies and realizing that the resulting triangle formed by that point, P1 and P3 is isosceles.
My contention is that, in the situation shown in Figure 3, Coulomb's law for stationary charges in Σ must be modified as follows to obtain the force between q1 and q2 as measured by co-moving springs:
(Equation 2)
This Coulomb law for moving charges can alternatively be formulated in terms of sphere densities. If λ1 is the sphere density on r of the spheres around q1, and λ2 is the sphere density on r of the spheres around q2, then:
(Equation 3)
[PS: As indicated here, a more general analysis shows that the two densities that need to be considered are the density of q1 spheres over r (a) along the line connecting the two charges on the side facing towards q2 and (b) along the line connecting the two charges on the side facing away from q2 . The result in the case of two charges moving at the same velocity is the same, but in more general situations this is the approach that must be taken.]
Equation 2 constitutes a fundamental law in my sphere model of electricity as it is simple, plausible, empirically correct, and very powerful:
Equation 2 constitutes a fundamental law in my sphere model of electricity as it is simple, plausible, empirically correct, and very powerful:
1) The law could hardly be any simpler. It is nicely symmetrical and, in addition to the concept of electric charge, Equation 2 merely includes two basic sphere model parameters: the number of spheres that cut through r and the angle at which they cut through r. The sine of that angle and the sphere numbers are simple factors in Equation 2.
2) Equation 2 is plausible as it represents a plausible generalization of Coulomb's law for charges that are stationary in Σ.
I have already set out here why the addition of the factor nΣ2/n1n2 is a natural generalization of Coulomb's law to moving charges.
As for the factor 1/sin2β, it can be seen in Figure 3 that r crosses each sphere shell along a path which is longer by the factor 1/sinβ than the shell's thickness, and this is true for both charges.
In the case of charges that are stationary in Σ, on the other hand, the path taken by r through each shell corresponds to the shell's thickness. Apparently what matters is each shell's local thickness, so r in the Coulomb law for moving charges must be normalized by multiplying it by sinβ.
3) The proposed law is empirically correct in the sense that it gives the same force as the tried and tested classical theories of electromagnetism and special relativity. This can be seen by determining the sphere density on a straight line emanating from a moving charge as a function of v, c and the angle α between that line and the vector v, by applying the cosine rule to the triangle P1P2P3 in Figure 2:
The term sinβ can also be expressed as a function of v, c and α, by applying the sine rule to the same triangle:
Inserting these expressions for the sphere density and sinβ into Equation 3 yields:
(Equation 4)
This equation is nothing but the result for the force between q1 and q2 as measured by co-moving springs obtained in classical theory, by applying Coulomb's law for stationary charges to q1 and q2 in the moving system and taking into account relativistic length contraction.
Therefore, if classical theory is empirically correct, then so is my Coulomb law for moving charges.
4) Equation 2 is very powerful because it has momentous consequences. If it is accepted as fundamental, Equation 4 follows and with it electric length contraction by the relativistic factor in the direction of movement, and in that direction only.
And that's not all. My sphere model implies the independence of the speed of light from the movement of its source, in other words two light signals emitted from the same location in the same direction will always travel side by side regardless of the relative speed of the sources of the light. Together with length contraction, this implies time dilation by the relativistic factor if light clocks of any orientation are used.
And that's still not all because length contraction and time dilation by the relativistic factor together imply all of special relativity, including the constancy of the two-way speed of light in all inertial frames of reference and including the Lorentz transformations if clocks in all inertial frames of reference are Einstein-adjusted.
All of that follows from the simple, innocent-looking Equations 2 and 3. But some big questions remain.
Can I be sure that it is possible to generalize from "electric length contraction" and "light clock time dilation" by the relativistic factors to length contraction and time dilation in general?
Can the sphere model of electricity be generalized to describe and explain the interaction of charged particles in arbitrary states of motion relative to each other?
Can it be used to explain the full range of "magnetic" phenomena?
Can Equations 2 and 3 be explained in more fundamental terms than the somewhat ad hoc way in which I have introduced them?
What role, if any, might be played by models of how charged particles exchange information with each other?
I suspect I may only be able to answer these questions once I have gained a deeper understanding of existing models of electricity and magnetism, not to mention other areas of physics.
I intend to make a start by studying and reviewing W. Geraint V. Rosser's Interpretation of Classical Electromagnetism (1997).
Any suggestions for other relevant literature, whether in the comment section or by email, would be gratefully received.