In their article on "A Test Theory of Special Relativity: I. Simultaneity and Clock Synchronization" (1977), Reza Mansouri and Roman U. Sexl raise the question of whether there are any meaningful alternatives to applying Einstein's clock adjustment procedure in every uniformly moving frame of reference. In particular, they consider whether there might be a preferred "ether" frame in which it would be sensible to apply Einstein's procedure while all clocks in every other frame would be adjusted based on clock readings in the preferred frame.
The authors begin by suggesting that the cosmic background radiation defines a system of reference which is a candidate for a possible "ether frame", but they do not explain how or why that might be the case.
Later in the article, the authors refer to a frame Σ in which Einstein's clock adjustment procedure and the slow transport clock adjustment procedure agree as an "ether frame". In the slow transport procedure, clocks in different locations are adjusted to the time shown by a single clock that is "slowly" moved to those locations. The slowness of the clock has to be established either by an existing set of clocks that have already been adjusted somehow, or by using the clock's "self-measured" speed: the distance it has traversed divided by the time that has passed as shown by the clock itself.
Once again it is not clear in what sense such a reference frame would constitute an "ether frame" if by "ether frame" the authors mean a frame in which Einstein-adjusted clocks are synchronized.
What is more, any suggestion that slow clock transport provides an independent way of adjusting distant clocks is somewhat undermined later in the article when the authors show that slow transport clock adjustment is equivalent to Einstein clock adjustment if and only if the empirically determined time dilation factor in Σ is given by its relativistic value. A slightly modified version of their proof can be found here.
In a nutshell, Mansouri and Sexl end up without any method of identifying a "preferred" system of reference in which we can be sure that Einstein-adjusted clocks have been synchronized at least locally.
They nevertheless consider what happens if we arbitrarily choose a frame Σ in which clocks are Einstein-adjusted and then adjust clocks in all other uniformly moving frames by comparing them with clocks in Σ, a procedure the authors call "external synchronization".
Specifically, they consider in some detail what happens if we adjust clocks in all other frames by setting them to zero when they pass a clock in Σ which shows zero:
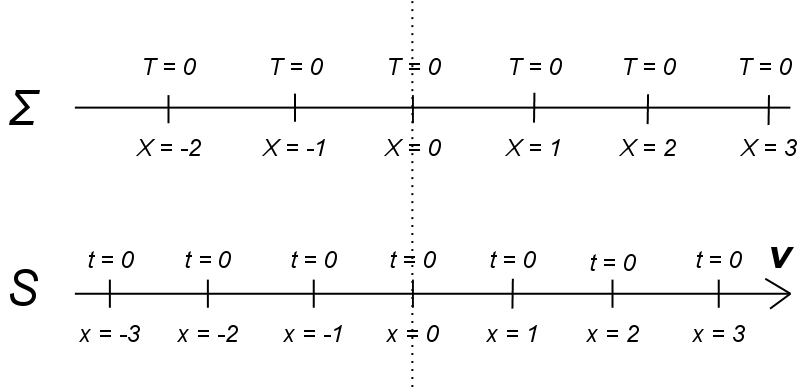
In this diagram, the time in Σ is T = 0 everywhere and all clocks in S take over that time from clocks in Σ as they pass them.
Mathematically, this amounts to setting the conventionality factor ε in the transformation equations between coordinates X, T in Σ and coordinates x, t in any frame S moving at v relative to Σ to ε = 0, yielding
t = aT
x = b(X - vT)
where a and b are the empirically determined time dilation and length contraction factors.
This transformation establishes "absolute simultaneity" according to the authors, by which they mean that events that have the same time coordinates in Σ also have the same time coordinates in S. It is important to note that the authors use the word "simultaneity" in a purely technical sense here to refer to equal time coordinates as measured by clocks which have not necessarily been synchronized.
Mansouri and Sexl observe that, if clocks are adjusted in this way, for an observer at rest in Σ moving clocks are slow and moving measuring rods shrink. Seen from a system S that moves relative to Σ, on the other hand, clocks in Σ are fast and measuring rods elongated, purely as a result of the way in which the clocks used to measure time have been adjusted. What is more, superluminal speeds are not ruled out and light moves at different speeds in opposite directions in all frames except Σ. These results, which can be formally deduced from the transformation equations, do not contradict special relativity because they depend on the way in which clocks have been adjusted.
So, is the choice of the conventionality factor just arbitrary and is any ε as good as any other? Mansouri and Sexl don't think so. With reference to special relativity's twin paradox, they point out that in the case of ε = 0 the explanation for the twins' difference in age varies depending on whether the unaccelerated twin is at rest in Σ or in some other frame S. The fact that the end result is the same "appears as a fortunate coincidence without deeper reason", and this "shows how the choice of unsuitable conventions can destroy the internal symmetry of a physical theory".
What the authors suggest here is that applying Einstein's clock adjustment procedure in all frames, which amounts to choosing ε = -v/c2, helps to reveal the "deeper reason" why the twin experiment has the same outcome regardless of which frame is the rest frame of the unaccelerated twin. This "deeper reason" is presumably the assumed equivalence of all uniformly moving frames of reference.
Against this, I would argue that neither Einstein clock adjustment in all frames nor the choice of ε = 0 in an arbitrarily chosen frame in which clocks have been Einstein-adjusted can reveal any "deeper reason" for the twin experiment outcome because both of these adjustment choices are just that: choices, decisions or conventions. In particular, it turns out that the special relativistic equivalence of the behaviour of moving clocks and measuring rods in all frames is not a fundamental fact of nature but an artifact created by a particular choice of clock adjustment.
It is true that this choice makes for a theory with great "internal symmetry", and maybe that's what makes it attractive to many. But, I would suggest, any investigation into the "deeper reason" for the twin experiment outcome would have to explore different avenues, such as the effects of different kinds of acceleration on matter or fields.
Despite this little niggle, it is clear that Mansouri and Sexl's article offers much greater insights into the role of convention in special relativity than any of the textbooks I have discussed in this blog. Like Einstein, the authors are perfectly clear about the fact that clock adjustment decisions are conventional. They go further by isolating what I have called the "conventionality factor" in the transformation equations between a first frame in which clocks have been Einstein-adjusted and other frames in which clocks are adjusted by some other means. They show that this factor ε represents an arbitrary element in the transformation equations as opposed to the empirically determined time dilation and length contraction factors a and b. And they show that this factor is the same for Einstein clock adjustment and slow clock transport adjustment if and only if a is given by its relativistic value.
All this is fascinating stuff. But there is one fundamental issue which the authors fail to address: which, if any, of the various clock adjustment procedures they discuss actually synchronizes distant clocks, and over what kind of distance? The authors vaguely suggest that there might be a preferred frame, possibly determined by the cosmic background radiation, in which Einstein's clock adjustment procedure can be deemed to synchronize any distant clocks. But they do not even hint at why or how that might be the case.
In previous posts I have explained why in general clocks in special relativity are not synchronized, why this leads to conceptual mayhem, and why the problem cannot simply be resolved by redefining "simultaneity". The issue can be illustrated by means of two clocks A and B spaced a few metres apart. I adjust the clocks by setting clock A to 1 o'clock and then walking over to clock B and setting clock B to 2 o'clock. I can then walk from clock B to clock A "arbitrarily fast" even if I take extended breaks, and I can even arrive at A "before I set off" from B, thus "reversing cause and effect", according to the clock readings on the two clocks. All this is, of course, a result of the fact that the two clocks have not been synchronized. So far none of the texts I have discussed addresses the basic distinction between clock adjustment procedures, which can be arbitrary, and clock synchronization procedures, which must meet additional criteria.
Enter Kevin Brown, who writes about the role of convention in relativity repeatedly and in depth in his recent book Reflections on Relativity (2010). What is more, Brown carefully develops his thoughts by charting the historical journey from Galileo and Newton to Einstein while at each stage discussing the logical structure of the theories set out by those scientists from a modern point of view.
Discussing Brown's analysis of the role of convention in relativity will therefore take some time. I'm going to make a start in my next post.
The authors begin by suggesting that the cosmic background radiation defines a system of reference which is a candidate for a possible "ether frame", but they do not explain how or why that might be the case.
Later in the article, the authors refer to a frame Σ in which Einstein's clock adjustment procedure and the slow transport clock adjustment procedure agree as an "ether frame". In the slow transport procedure, clocks in different locations are adjusted to the time shown by a single clock that is "slowly" moved to those locations. The slowness of the clock has to be established either by an existing set of clocks that have already been adjusted somehow, or by using the clock's "self-measured" speed: the distance it has traversed divided by the time that has passed as shown by the clock itself.
Once again it is not clear in what sense such a reference frame would constitute an "ether frame" if by "ether frame" the authors mean a frame in which Einstein-adjusted clocks are synchronized.
What is more, any suggestion that slow clock transport provides an independent way of adjusting distant clocks is somewhat undermined later in the article when the authors show that slow transport clock adjustment is equivalent to Einstein clock adjustment if and only if the empirically determined time dilation factor in Σ is given by its relativistic value. A slightly modified version of their proof can be found here.
In a nutshell, Mansouri and Sexl end up without any method of identifying a "preferred" system of reference in which we can be sure that Einstein-adjusted clocks have been synchronized at least locally.
They nevertheless consider what happens if we arbitrarily choose a frame Σ in which clocks are Einstein-adjusted and then adjust clocks in all other uniformly moving frames by comparing them with clocks in Σ, a procedure the authors call "external synchronization".
Specifically, they consider in some detail what happens if we adjust clocks in all other frames by setting them to zero when they pass a clock in Σ which shows zero:
In this diagram, the time in Σ is T = 0 everywhere and all clocks in S take over that time from clocks in Σ as they pass them.
Mathematically, this amounts to setting the conventionality factor ε in the transformation equations between coordinates X, T in Σ and coordinates x, t in any frame S moving at v relative to Σ to ε = 0, yielding
t = aT
x = b(X - vT)
where a and b are the empirically determined time dilation and length contraction factors.
This transformation establishes "absolute simultaneity" according to the authors, by which they mean that events that have the same time coordinates in Σ also have the same time coordinates in S. It is important to note that the authors use the word "simultaneity" in a purely technical sense here to refer to equal time coordinates as measured by clocks which have not necessarily been synchronized.
Mansouri and Sexl observe that, if clocks are adjusted in this way, for an observer at rest in Σ moving clocks are slow and moving measuring rods shrink. Seen from a system S that moves relative to Σ, on the other hand, clocks in Σ are fast and measuring rods elongated, purely as a result of the way in which the clocks used to measure time have been adjusted. What is more, superluminal speeds are not ruled out and light moves at different speeds in opposite directions in all frames except Σ. These results, which can be formally deduced from the transformation equations, do not contradict special relativity because they depend on the way in which clocks have been adjusted.
So, is the choice of the conventionality factor just arbitrary and is any ε as good as any other? Mansouri and Sexl don't think so. With reference to special relativity's twin paradox, they point out that in the case of ε = 0 the explanation for the twins' difference in age varies depending on whether the unaccelerated twin is at rest in Σ or in some other frame S. The fact that the end result is the same "appears as a fortunate coincidence without deeper reason", and this "shows how the choice of unsuitable conventions can destroy the internal symmetry of a physical theory".
What the authors suggest here is that applying Einstein's clock adjustment procedure in all frames, which amounts to choosing ε = -v/c2, helps to reveal the "deeper reason" why the twin experiment has the same outcome regardless of which frame is the rest frame of the unaccelerated twin. This "deeper reason" is presumably the assumed equivalence of all uniformly moving frames of reference.
Against this, I would argue that neither Einstein clock adjustment in all frames nor the choice of ε = 0 in an arbitrarily chosen frame in which clocks have been Einstein-adjusted can reveal any "deeper reason" for the twin experiment outcome because both of these adjustment choices are just that: choices, decisions or conventions. In particular, it turns out that the special relativistic equivalence of the behaviour of moving clocks and measuring rods in all frames is not a fundamental fact of nature but an artifact created by a particular choice of clock adjustment.
It is true that this choice makes for a theory with great "internal symmetry", and maybe that's what makes it attractive to many. But, I would suggest, any investigation into the "deeper reason" for the twin experiment outcome would have to explore different avenues, such as the effects of different kinds of acceleration on matter or fields.
Despite this little niggle, it is clear that Mansouri and Sexl's article offers much greater insights into the role of convention in special relativity than any of the textbooks I have discussed in this blog. Like Einstein, the authors are perfectly clear about the fact that clock adjustment decisions are conventional. They go further by isolating what I have called the "conventionality factor" in the transformation equations between a first frame in which clocks have been Einstein-adjusted and other frames in which clocks are adjusted by some other means. They show that this factor ε represents an arbitrary element in the transformation equations as opposed to the empirically determined time dilation and length contraction factors a and b. And they show that this factor is the same for Einstein clock adjustment and slow clock transport adjustment if and only if a is given by its relativistic value.
All this is fascinating stuff. But there is one fundamental issue which the authors fail to address: which, if any, of the various clock adjustment procedures they discuss actually synchronizes distant clocks, and over what kind of distance? The authors vaguely suggest that there might be a preferred frame, possibly determined by the cosmic background radiation, in which Einstein's clock adjustment procedure can be deemed to synchronize any distant clocks. But they do not even hint at why or how that might be the case.
In previous posts I have explained why in general clocks in special relativity are not synchronized, why this leads to conceptual mayhem, and why the problem cannot simply be resolved by redefining "simultaneity". The issue can be illustrated by means of two clocks A and B spaced a few metres apart. I adjust the clocks by setting clock A to 1 o'clock and then walking over to clock B and setting clock B to 2 o'clock. I can then walk from clock B to clock A "arbitrarily fast" even if I take extended breaks, and I can even arrive at A "before I set off" from B, thus "reversing cause and effect", according to the clock readings on the two clocks. All this is, of course, a result of the fact that the two clocks have not been synchronized. So far none of the texts I have discussed addresses the basic distinction between clock adjustment procedures, which can be arbitrary, and clock synchronization procedures, which must meet additional criteria.
Enter Kevin Brown, who writes about the role of convention in relativity repeatedly and in depth in his recent book Reflections on Relativity (2010). What is more, Brown carefully develops his thoughts by charting the historical journey from Galileo and Newton to Einstein while at each stage discussing the logical structure of the theories set out by those scientists from a modern point of view.
Discussing Brown's analysis of the role of convention in relativity will therefore take some time. I'm going to make a start in my next post.