The two-way speed of light

Up until now I have chiefly looked at some conceptual issues relating to special relativity: How do physicists choose to adjust distant clocks? What do they, therefore, mean when they state that the one-way speed of light is constant for every observer? What consequences do their decisions and definitions have for the applicability of concepts such as simultaneous existence, one-way speed and causality in the framework of special relativity?

Interesting and important as I believe these issues are, it is now time to turn to the physical substance of special relativity. At the heart of this lies the empirical finding that the two-way or round-trip speed of light is the same in every spatial inertial coordinate system.

Albert Einstein showed that the constancy of the two-way speed of light implies all of special relativity, including length contraction and time dilation by the relativistic factors for moving bodies in any spatial inertial frame of reference in which clocks are Einstein-adjusted.

Helmut Günther has shown that, conversely, length contraction and time dilation by the relativistic factors for moving bodies in any particular spatial inertial frame of reference in which clocks are Einstein-adjusted implies all of special relativity, including the constancy of the two-way speed of light.

To see more directly that length contraction and time dilation implies the constancy of the two-way speed of light, consider a first spatial inertial frame of reference Σ in which light propagates in symmetrical conditions in opposite directions so that we can use Einstein's clock adjustment procedure to synchronize clocks in that frame.

The two-way speed of light c' in a second frame of reference S moving at v relative to Σ can then be worked out as follows:

In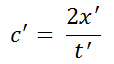


we know that

where t1 and t2 are the to-and-fro times in Σ which the light needs to travel along the to-and-fro path 2x' in S.
From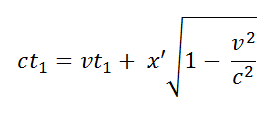

and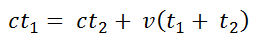


we find that

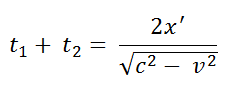It follows that


In this blog, I will follow Günther in regarding length contraction and time dilation as fundamental and the constancy of the two-way speed of light as a consequence. Speed measurements are, after all, based on measurements of length and time, so to explain the constancy of the two-way speed of light it seems useful to explore what we know about the behaviour of measuring rods and clocks in different spatial inertial coordinate systems.

The question of how the constancy of the two-way speed of light can be explained can then be rephrased as follows: how can we explain length contraction and time dilation for moving bodies in any spatial inertial frame of reference in which light propagates in symmetrical conditions and clocks have been synchronized using Einstein's method?

Moving bodies move relative to a frame of reference in which light propagates in symmetrical conditions because at some point they have undergone local acceleration relative to that frame, and that is the only action that has been performed on them that could explain length contraction and time dilation. My question could thus finally be expressed as follows: how does local acceleration in such frames cause bodies to contract in the direction in which they have been accelerated, and how does it cause clocks to go slow?

Expressed in this way, it seems to me that, once conceptual issues have been sorted out, much of the remaining mysteriousness of special relativity vanishes. As discussed in previous posts, the local acceleration of any particle surrounded by, for example, an electromagnetic field distorts that field and may thus well have an effect on the length of any body containing such particles, and on the duration of any periodic processes involving that particle.

What is more, the speed at which field disturbances propagate through the field, in other words the speed of light c, can be expected to influence those length and time effects because it has a bearing on the distortion of the field.

The remaining question is then simply how acceleration to a particular speed v in a frame of reference in which light signals propagate in symmetrical conditions changes length and time measurements precisely in accordance with the relativistic length contraction and time dilation factors. And this is the question to which I now intend to turn.

Convention in relativity - my findings

Over the last two years, I have devoted a fair amount of time to studying the issue of convention in special relativity, in particular the role played by convention in the principle of the constancy of the speed of light for every observer, and it is now time to pull my findings together. The summary below contains links to other posts in which I expand on the points made - readers who want to consult those posts may want to right-click on the links to open them in separate tabs.

Fundamentally, the concept of one-way speed relies on the notion of simultaneity in different points and thus on our ability to adjust clocks in different points in a manner which synchronizes them.

I have argued that the concept of simultaneity in different points, or of clock synchronization, is linked to the concept of symmetry as follows:

Two distant clocks in a spatial inertial coordinate system can be synchronized by emitting identical signals in opposite directions from the mid-point between the clocks and adjusting the clocks to the same time when the signals arrive there, provided the conditions in which the two signals are emitted and propagate are symmetrical.

This is not just a concept of simultaneity I have dreamt up. It is the standard concept of simultaneity to which physicists and others have subscribed for hundreds of years and which, through its links with other concepts such as causality, one-way speed and simultaneous existence, is firmly anchored in the English language. Yet physicists and philosophers have paid surprisingly little attention to the requirement of symmetry in the conditions of signal transmission.

Albert Einstein is a notable exception. In one of his articles, he insisted that, for a clock adjustment procedure using signals to qualify as a synchronization procedure, the means of sending signals "must be such that we have no reason to believe that the phenomena of signal transmission in the direction AB differ in any way from the phenomena of signal transmission in the direction BA".

As I have shown in detail here and here, ignoring this requirement may lead to conceptual mayhem.

But establishing whether or not that requirement is fulfilled in any particular spatial inertial frame of reference for any particular type of signal can be more difficult than meets the eye.

Suppose we follow Einstein in using light signals to adjust clocks in accordance with the synchronization procedure set out above. Suppose that to the best of our knowledge light signals propagate in symmetrical conditions in opposite directions in a first frame of reference. Suppose that, for example, all electric and other measurable fields surrounding stationary particles are found to be spherically symmetrical and all macroscopic conditions of signal emission and transmission are found to be symmetrical, too. Then it would appear that those signals can be used to synchronize clocks in that frame of reference.

But those very same signals can then not be used to synchronize clocks by an observer who is moving relative to that frame of reference, since her movement in one particular direction inevitably breaks the symmetry of the conditions of signal emission and/or propagation.

We might think the problem could be overcome by the observer in the second frame sending out her own light signals. But that wouldn't help because empirically they would be found to travel in tandem with the signals sent out in the first frame of reference and are therefore not suitable, either.

So we might be tempted to conclude that Einstein's clock adjustment procedure does not synchronize clocks in the moving frame of reference.

But what if, as physicists assure us, the conditions of signal transmission in the second frame of reference appear to be symmetrical, too? What if all electric and other measurable fields surrounding stationary particles are found to be spherically symmetrical and all macroscopic conditions of signal transmission are found to be symmetrical in that frame, too?

Then it would appear that observers in both frames of reference would be equally entitled, or rather equally ill-placed, to claim that Einstein's procedure synchronizes clocks in their frame of reference.

All we can then say is that if the procedure synchronizes clocks in the first frame, then it does not synchronize clocks in the second, and vice versa, because the requirement of symmetry can only be met in at best one of the frames. But we do not know in which, if in any.

Max Born concluded from this that we might as well use Einstein's procedure to adjust clocks in any inertial frame of reference. And this may well be justified on pragmatic grounds.

But - and this is my key finding - it leaves us with a theory in which in general clocks are not synchronized.

Could we perhaps, as suggested by Einstein, resolve the problem by declaring clocks adjusted in this manner to be synchronized by definition or by convention? The answer is "no" because what is conventional is our choice of clock adjustment procedure and not our choice of synchronization procedure. Even if we agree on a technical definition of "simultaneity (physics)" = "equal time coordinates as measured by Einstein-adjusted clocks", this does not resolve the conceptual problems caused by using a clock adjustment procedure which ignores the requirement of symmetry.

In fact, the apparently widespread belief that Einstein's 1905 clock adjustment procedure is a synchronization procedure, or can be declared to be one "by definition", has led some physicists to draw spectacular but misguided conclusions on issues such as causality and existence. These conclusions are the result of what I have called the "simultaneity syndrome" in modern physics: the continued and uncritical application of concepts depending on synchronization, such as one-way speed, causality and distant simultaneous existence, in the framework of a theory in which clocks have not in fact been synchronized.

Some of the more lucid writers on special relativity seem to have sensed that Einstein's clock adjustment procedure may not be the most obvious choice to qualify as a synchronization procedure. They have therefore come up with a number of alternative and supposedly more intuitive clock adjustment procedures, such as slow clock transport or the requirement that observers in different frames of reference agree on their speed relative to each other. The most persuasive alternative is perhaps to go back to the procedure implicit in Newton's laws, using objects as signals rather than light.

The problem with all of these procedures is that they are perfectly equivalent with Einstein's procedure and therefore they are not synchronization procedures, either.

That is not to say that they are useless. As a number of writers from Henri Poincaré and Albert Einstein to Kevin Brown and Helmut Günther have pointed out, we may want to choose a clock adjustment procedure which makes the laws of physics particularly simple, and that's what all the procedures mentioned above do: they lead to the familiar symmetrical laws of mechanics and they ensure that Maxwell's equations of electromagnetism are valid in any inertial frame of reference.

We just need to bear in mind that, in the framework of a theory based on such a clock adjustment procedure, clocks are not necessarily synchronized. As a result, in such a theory events with equal time coordinates are not necessarily simultaneous; one-way "speeds" are potentially meaningless "coordinate speeds measured with clocks which are not necessarily synchronized"; and the concept of causality may not be applicable when "superluminal speeds" are involved.

Then everything falls into place: the principle of the constancy of the "speed of light" for every observer, for example, since it becomes clear that the "speed" it refers to is a purely formal "coordinate speed" obtained from clocks which are not necessarily synchronized; or the "time quakes" which occur in special relativity when distant observers begin to move relative to each other, since, again, the only "time" that is subjected to such swings is a purely formal "coordinate time" shown by clocks which are not synchronized.

Ultimately it may thus seem that the strangeness of special relativity does not correspond to anything in the observed phenomena but is purely the result of a clock adjustment procedure which is not a synchronization procedure. In other words, the world may not actually be half as weird as a superficial reading of some physics books might suggest. And it may seem that I could therefore stop right here and close this blog, job done.

But I can't. Special relativity includes a number of fairly strange statements which are independent of any clock adjustment procedure. These include the empirical facts that the two-way speed of light is found to be the same in every spatial inertial frame of reference if clocks of identical construction are used, and that a twin who makes a round-trip will be younger on her return than her sibling who stayed at home all the while.

These are facts which are not necessarily entirely expected and which therefore call for an explanation. So there remains some work to be done for me.

A lot of work. Because I believe that in order to arrive at such an explanation I will first have to gain a much better understanding of some areas of physics than I currently possess. I mention only classical electrodynamics, quantum electrodynamics and general relativity. At least that's what I imagine.

And there is more. I have complained the length and breadth of this blog that Einstein's clock adjustment procedure is not a synchronization procedure, but have I been able to offer a meaningful alternative? I have not.

I have talked about the possibility that the "acceleration history" of a source of light could be a parameter which is missing from the laws of nature as currently formulated and which may help to determine whether or not the conditions in which light propagates in opposite directions from that source are symmetrical.

In that context I have developed a rudimentary "sphere model" of electricity which would seem to explain the fact that the speed of light is locally independent of the uniform movement of the source of the light in a spatial inertial frame of reference.

But these are feeble attempts compared to the magnitude of the task.

I think a good starting point to take my inquiries further is the constancy of the two-way speed of light for all inertial observers. How have physicists explained it? How would I explain it? Is it even a phenomenon that can be explained or must it be accepted as a fundamental fact of nature? I think it would be reasonable to expect a relatively long wait before my next post.

Kevin Brown on convention in relativity

In his book Reflections on Relativity (2010), Kevin Brown talks about the light speed principle in special relativity in great detail. He makes careful distinctions between what is empirical fact and what is conventional or a matter of decision-making. He acknowledges that different choices are possible and that there are and always have been debates among physicists on which of these are preferable. And he engages with those debates.

All of this makes his book a pleasure to read for somebody who has long felt that there is much more to relativity than what most textbooks tell their readers. Somebody who, as a student, despaired of an approach to the teaching of physics which allowed no room for debate or questions. Somebody who, years later, by writing this blog, is trying to gain a deeper understanding of special relativity than he could ever have hoped to gain as an undergraduate.

And there is more. Kevin Brown, with his knowledge of the historical background, his awareness of conceptual issues and his grasp of technical details, clearly comes down on the side of Newton and Einstein on the issue of simultaneity, and thus on the side of Einstein's light speed principle. Which makes his writings an ideal test for a sceptic like myself.

Brown makes it clear early on in his book that there is a choice regarding time coordinates. He says one possibility is to choose them so that inertia is isotropic, in other words "the force required to accelerate an object from rest to a given speed is the same in all directions". This "effectively establishes the planes of simultaneity of inertial coordinate systems".

Brown's main argument in favour of time coordinates which ensure inertial isotropy is that they lead to "the usual symmetrical laws of mechanics" and are therefore "the most intuitive, convenient, and readily accessible systems" (pp. 24-27).

Elaborating on these ideas, he approvingly quotes Henri Poincaré as saying in 1898 that we naturally choose our coordinate systems "in such a way that the statements of the natural laws are as simple as possible", and according to Brown that "almost invariably means inertial coordinates". "We simply choose, of our own free will, to use inertial coordinates - with the corresponding inertial definition of simultaneity - because this renders the statement of physical laws and the descriptions of physical phenomena as simple and perspicuous as possible, by taking advantage of the maximum possible symmetry," Brown insists. The constancy of the speed of light in terms of such coordinates is then "an empirical fact" (pp. 290-291).

Brown acknowledges, however, that "it could be argued that a total unique temporal ordering of events is a more useful organizing principle than the isotropy of inertia". This is true "especially if we regard the total temporal ordering of events as a requirement of intelligibility". But, Brown goes on, that approach "suffers from a certain inherent lack of conviction, because while asserting the ontological reality of anisotropy in all but one (unknown) frame of reference, it unavoidably requires us to disregard that assertion and arbitrarily assume one particular frame as being 'the' rest frame" (pp. 292-293).

Brown's account adds up to a very detailed, clear and persuasive argument for choosing time coordinates in accordance with Einstein's or Newton's clock adjustment procedures, which turn out to be equivalent.

But there is a question which Brown does not address directly. Like all the other authors discussed in this blog, Brown says events with equal time coordinates as measured by Einstein- or Newton-adjusted clocks are "simultaneous" without exploring or explaining why that should be the case. However, unlike any of the authors discussed before, Brown drops a number of hints suggesting that there may in fact be a problem with "simultaneity" in special relativity.

One of these hints is his acknowledgment that choosing time coordinates in accordance with Einstein's or Newton's clock adjustment procedure may lead to a problem of "intelligibility". Sadly, Brown does not explore what this problem consists in and how it comes about.

My own view is, of course, that Einstein's and Newton's clock adjustment procedures - for all their benefits in terms of simplicity and symmetry - lead to a situation in which equal time coordinates do not invariably imply a relationship of simultaneity. And that this fact renders the resulting theory unintelligible unless it is made explicit and its repercussions on the applicability of concepts that rely on the concept of simultaneity are explored and explained.

Brown indirectly addresses some of these repercussions in a chapter on "The Breakdown of Simultaneity". He points out that, if Einstein's or Newton's clock adjustment procedure are used, an accelerated observer may find that one and the same distant event "is assigned multiple times of occurrence" (p. 313). I'd suggest that this would only pose a problem if we took the meaning of "simultaneity" in relativity seriously, because we'd then have to conclude that for such an observer certain events do not just appear to occur but really do occur several times over, which is nonsense. The problem resolves itself if we realise that, in general, equal time coordinates in relativity do not imply a relationship of simultaneity in the first place.

Another hint in Brown's book that the concept of simultaneity in relativity may be flawed is his acknowledgment that Einstein's clock adjustment procedure relies on the assumption of "memorylessness", in other words the idea that an elementary particle does not "somehow 'remember' its entire history of accelerations and thereby 'know' its present absolute velocity relative to a common fixed reference" (p. 53). The potential importance of a particle's acceleration history is of course something I have emphasized in previous blog posts (for example here), although I have not used expressions such as "memory" or "remembering".

Again, sadly, Brown does not develop this point beyond mentioning that "Weyl's unified field theory" was apparently built on the premise that particles can remember their acceleration history. Unfortunately I have not been able to find any documentation on that theory to see how it relates to my own ideas.

The possibility that a particle's acceleration history may determine whether or not light emitted by that particle propagates in symmetrical conditions in all directions is also relevant to Brown's assertion that a total temporal ordering would require us to "arbitrarily" choose one frame of reference in which light is deemed to propagate isotropically. If the assumption of "memorylessness" were wrong and if we knew something about the acceleration history of a system of particles we want to study, then perhaps our choice of reference frame in which light is deemed to propagate in symmetrical conditions would not have to be entirely arbitrary. And we might find that there is not just one but many frames of reference in which light locally propagates in symmetrical or at least broadly symmetrical conditions.

Brown's book thus contains a number of pointers regarding the issue of convention in the light speed principle which I intend to follow up in this blog over the years and decades to come.

Before I conclude this post, I would like to mention another book which I have come across recently and which is just as clear as Brown's on the element of convention in the light speed principle, but which has similar limitations regarding the meaning of "simultaneity" in relativity.

This is the textbook "Special Relativity - A new way into Einstein's world" by Helmut Günther (2007). The author says he wants to break with traditional introductions to special relativity which "start by confronting unsuspecting readers with the incredible postulate of the universal constancy of the speed of light - Einstein's principle of relativity - and then leave them to lose themselves in endless musings about the no less incredible consequences concerning the behaviour of moving measuring rods and clocks" (p. 7).

An excellent plan!

Günther proceeds to give due prominence to the role of clock adjustment procedures in the light speed principle and shows how the Lorentz transformations and Einstein's whole theory can be derived very simply by:

a) adjusting clocks in a first frame of reference Σ using Einstein's clock adjustment procedure;

b) requiring clocks in any other frame of reference S moving at v relative to Σ to be adjusted such that Σ is measured to be moving at -v from the point of view of S - Günther calls this the "elementary principle of relativity";

c) finding empirically that the time dilation and length contraction factors in Σ have the values they have in special relativity (pp. 36-60).

All that is very clear and very interesting.

But an important pillar of the whole edifice crumbles in a single sentence on page 36, where Günther asserts that "in principle" we are "free to agree how to synchronize clocks" in the S frames. He adds that we are in fact well-advised to follow Henri Poincaré in choosing a procedure which makes the transformation formulas particularly simple and symmetrical, and that it is therefore sensible to apply b) above.

We are "free to agree how to synchronize clocks"? Really? So, if we agree to "synchronize" two clocks at opposite ends of a table by setting one to 1 o'clock and the other to 2 o'clock, then we have in fact synchronized them? That's plain nonsense because, at the risk of repeating myself, not every clock adjustment procedure is a synchronization procedure! And there is no reason to believe - and Günther does not even try to make that case - that the clock adjustment procedure implicit in b) above actually synchronizes clocks in the S frames.

So, Günther, for all his best intentions, ends up still confronting unsuspecting readers with a rather incredible claim, namely that his "elementary principle of relativity" has anything to do with synchronizing clocks!

And that concludes my review of the literature on the role of convention in the light speed principle.

Of course, if any of my readers think that there are important publications on the issue which I have failed to mention, I'd love to hear about them.

In the meantime, I'd recommend the following to anybody trying to gain a proper understanding of the special theory of relativity:

READ Albert Einstein, read Reza Mansouri/ Roman U. Sexl, read Kevin Brown and read Helmut Günther. Pay particular attention to their explanation of the role of convention in the light speed principle, because convention plays an important role in that principle and all the above-mentioned authors are very clear about that.

BUT replace every mention of "synchronization" in those publications with "clock adjustment", every mention of "simultaneous events" with "events with equal time coordinates" and every mention of "speed" with "coordinate speed using clocks which are not necessarily synchronized".

AND do not fall into the trap of the simultaneity syndrome, in other words be aware that any concepts that rely on synchronization, such as one-way speed, causality and simultaneous existence, have at best limited applicability in special relativity.

THEN you should be well-placed to begin to make sense of it all.

A fuller summary of my findings to date, and a glimpse of which questions I am going to address next, will have to wait until my next post.

Newton's idea of simultaneity

If, as Kevin Brown says in his book on relativity, Einstein's clock adjustment procedure using light signals leads to the same clock adjustment as Newton's clock adjustment procedure using objects, it is worth investigating whether or not Newton's procedure is a synchronization procedure, in other words whether or not it ensures that events with equal time coordinates are simultaneous.

From a purely logical point of view, it is clear that in general Newton's procedure cannot be a synchronization procedure because I have already shown, here and in subsequent posts, that in general Einstein's procedure is not a synchronization procedure.

But it would be nice to be able to see that directly, by examining Newton's procedure more closely.

In Newton's procedure - or more precisely the procedure which is implicit in his laws of mechanics - two clocks A and B in a first spatial inertial system S1 are adjusted to show the same time when identical objects projected in opposite directions from the mid-point between A and B using identical acceleration mechanisms arrive at those clocks, provided the conditions in which the objects are accelerated and in which they travel are symmetrical in both directions. Events with equal time coordinates in S1 are then simultaneous by virtue of the very meaning of simultaneity.

The crucial question is how we can then adjust clocks in a second spatial inertial system S2 that moves relative to the first. According to Newton, we can do that by accelerating the clocks, the objects and the accelerating mechanisms used in S1 so that they come to rest in S2 and performing the same procedure in S2 to adjust distant clocks in that system.

Let's assume that in both frames the procedure is performed in "empty space", notably in the absence of any medium such as air which might disturb the symmetry of the conditions in which the objects are accelerated or travel.

But even in the absence of any medium such as air, after the clocks, the acceleration mechanisms and the objects have been accelerated in one particular direction, are the conditions in which the procedure is then performed in S2 still symmetrical in opposite directions?

Newton evidently thought they were. And it's easy to see why. Newton didn't know that "empty space" is in fact filled with all manner of fields which surround any object. To him, the objects used in S2 would be just the same objects as they were in S1 and the symmetry of the conditions of any further acceleration and movement in opposite directions would not have been disturbed by their acceleration from S1.

That is why he thought that, as measured by Newton-adjusted clocks in S1, two identical objects at rest in S2 would undergo the same acceleration if they were projected in opposite directions using identical acceleration mechanisms. Today we know that this is not the case.

And that does not come as a surprise given that today we know that all objects are surrounded by, for example, electromagnetic fields. We also know that disturbances in such fields need some time to travel over any closed path.

Let's take the example of a simple electron whose field is spherically symmetrical in S1 and let's see how that field is affected if the electron is accelerated locally, for example as the result of a collision.

Qualitatively, and without adjusting any clocks, any field disturbance can be expected to propagate symmetrically around the electron's original position of rest, but the movement of the electron in one particular direction then creates asymmetrical conditions in the field surrounding it.

Quantitatively, let's assume that at a time t1 in S1 an electron at rest in S1 and surrounded by a spherically symmetrical field undergoes such a sudden acceleration to a speed v.

The field is represented here by a series of concentric spheres surrounding the electron. At the time t2 > t1 in S1, the electron moves at v and information about its acceleration is spreading outwards through the electron's field. Each of the spheres surrounding the electron starts to move at v when the information about the acceleration reaches it, leading to the following situation at the time t2:

As the information spreads further, the area around the electron in which the sphere density is asymmetrical grows:

At the boundary between areas of different density, shown in red, an electromagnetic signal propagates away from the electron (for details on how this happens, see Lesson 4 in this document by Daniel V. Schroeder). Any further sudden acceleration of the electron would give rise to a new electromagnetic signal. And the light speed law appears to be that any acceleration information always traverses the same number of spheres in the same amount of time. This means that locally in S1 the speed of an electromagnetic wave is independent of the speed of the light-emitting body.

The sphere model illustrates the fact that if the field around an electron, and thus around any object containing electrons, is symmetrical, then the field around the same electron accelerated locally to a speed v is no longer symmetrical. And for that reason Newton's clock adjustment procedure applied in a second frame S2 moving at a speed v relative to S1 is not a synchronization procedure.

At least not locally. Over cosmic distances, Newton's or Einstein's procedure may well be applicable to sets of clocks that move at a speed v relative to one another. The reason for that is that clocks that are very distant from each other may be moving relative to each other as a result of certain kinds of acceleration which disturb the local fields around them only negligibly. As far as I understand it, cosmic expansion and gravity are examples of such locally non-perturbative accelerations:

Locally, however, all particles or objects are subjected to the same gravitational or cosmic expansion influences. Therefore, if they move relative to each other locally then that must be the result of previous local accelerations which have disturbed the electric fields surrounding them.

My investigation into whether or not Newton's clock adjustment procedure is a synchronization procedure has led me to develop my sphere model of electricity and light propagation a bit further in this post.

After these flights of fancy, it is time to test my thoughts against the best of the literature on simultaneity in Newton's and Einstein's theories. And that leads me straight back to Kevin Brown's book Reflections on Relativity. In my next post.