So, what do Mansouri and Sexl mean when they say that "a theory maintaining absolute simultaneity is equivalent to special relativity"? Are they right? And what, if anything, does that tell us about the role of convention in Einstein's light speed principle?
First, let's see how Mansouri and Sexl approach the issue. They begin by assuming that Einstein's clock adjustment procedure has been applied in a first frame of reference Σ. The authors then consider a second frame S whose origin moves at v < c with respect to Σ, as measured with standard rods and clocks in Σ. They assume that the relationship between coordinates (X, T) in Σ and (x, t) in S is linear and they express that relationship in the following form:
t = aT + εx
(1)
x = b(X - vT)
It is striking that, rather than opting for a standard linear transformation in which t and x are represented in terms of T and X:
t = AT + BX
(2)
x = CT + DX
Mansouri and Sexl choose to present t as a function of T and x. (1) and (2) are equivalent in the sense that a, ε, b and v can be expressed in terms of A, B, C and D and vice versa. The reason why the authors use (1) rather than (2) is that the factors a, b, v and ε have special significance. As Mansouri and Sexl point out, a and b represent "the time dilatation and length contraction factors", which may depend on v and are a matter of empirical fact, while "arbitrary values of ε can be achieved" by choosing a suitable clock adjustment mechanism.
To see why b can be interpreted as a "length contraction" factor, consider the following diagram:
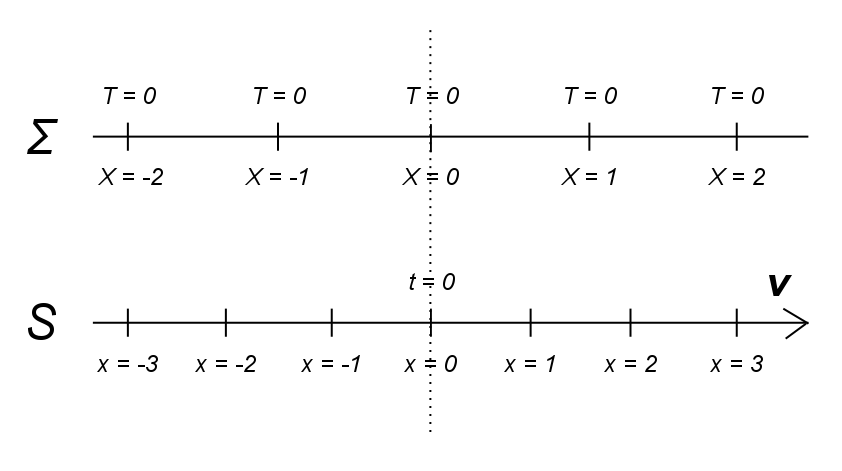Figure 1
In this diagram, clocks in Σ have been Einstein-adjusted, so in Σ time coordinates are well-defined in any location. In S, by contrast, distant clocks have not yet been adjusted, so we can only specify a time for a single clock. We choose that clock to be the one located at x = 0 and set it so that (x, t) = (0, 0) in S and (X, T) = (0, 0) in Σ coincide.
Now, it may be found empirically that any x differs from the X with which it coincides by a particular factor. Assuming that movement at v relative to Σ affects measuring rods at any location in S equally compared to identical measuring rods in Σ, this length contraction/dilation factor is the same for any pair of coinciding coordinates x, X in Figure 1 and also for any coinciding lengths l in S and L in Σ. Inserting T = 0 in (1), we obtain x = bX, so b is that length contraction/dilation factor.
To see that a is the time dilation factor, consider the following diagram, which shows the situation of Figure 1 after the Time T1 has passed in Σ:
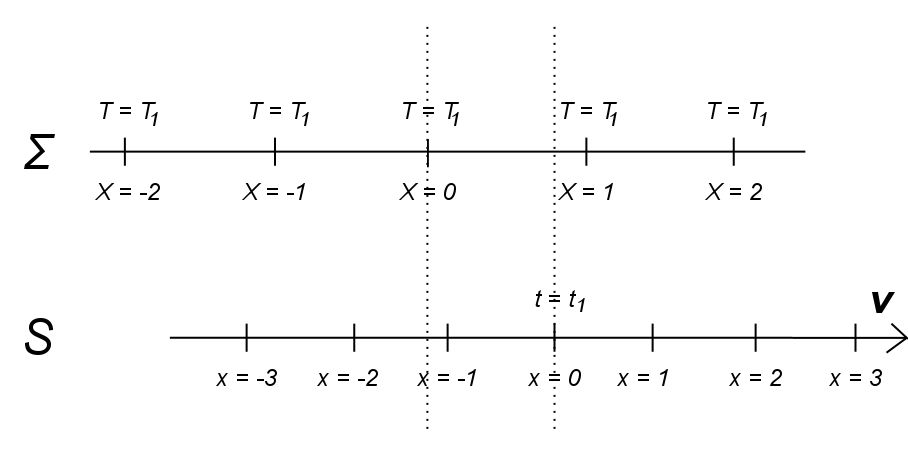Figure 2
It may be found empirically that t1 differs from T1 by a particular factor. Assuming that movement at v relative to Σ affects clocks equally at any location and time in S, this time contraction/dilation factor is the same for any single clock in S passing a series of clocks of identical construction in Σ. Inserting x = 0 in (1), we obtain t1 = aT1 , so a is that time contraction/dilation factor.
And that's all in the relationship between S coordinates and Σ coordinates that is a matter of empirical fact. How we set the time on clocks in S in locations other than x = 0 is a matter of choice, preference, decision-making, convention... and that choice is expressed mathematically in the value of ε, which may in fact be chosen to be a function of x as well as v. In terms of the factors occurring in (2) it can be expressed as ε = B/D, while b = D, v = -C/D and a = BC/D - A.
As Mansouri and Sexl point out, the value of ε in special relativity is -v/c2. This value can be called "relativity's conventionality factor". It was chosen by Einstein because it ensures that the one-way speed of light is the same for every observer in every frame of reference, which in turn ensures that the laws of physics take on a particularly simple form.
But what if a different value is chosen, say ε = 0 for any reference frame moving at any speed v relative to Σ? Mansouri and Sexl state that this particular case leads to a theory maintaining absolute simultaneity. What they mean by that is that, in the framework of this theory, two events that have the same time coordinate in a frame S moving at v relative to Σ also have the same time coordinate in any other frame S' moving at v' relative to Σ. In other words, if two events have coordinates (t1, x1) and (t2, x2) in S and (t1', x1') and (t2', x2') in S', then t1 = t2 if and only if t1' = t2'. This follows from ε = 0 in (1) by first transforming t1 and t2 into T1 and T2 in Σ and then T1 and T2 into t1' and t2' in S'.
Mansouri and Sexl add that a theory in which the conventionality factor is set to ε = 0 is "equivalent to special relativity" in the sense that if the outcome of an experiment can be predicted correctly using special relativity, then it can also be predicted correctly using a theory in which ε = 0, and vice versa. This is no doubt true because the conventionality factor merely expresses how we have chosen to adjust distant clocks and that does not in and of itself tell us anything about the world.
Nevertheless, Mansouri and Sexl dismiss the choice of ε = 0 as an "unsuitable" convention. Their reasons for this conclusion and the implications for the role of convention in the light speed principle will be the subject of my next post.
The article "A Test Theory of Special Relativity: I. Simultaneity and Clock Synchronization"
by Reza Mansouri and Roman U. Sexl, published in 1977, contains at
least two statements that are pertinent to my current investigation into
the role of convention in Einstein's light speed principle.
The
first is that "one of the most debated problems in special relativity
is the role of convention in the definition of simultaneity of distant
events and the related question of first-order experiments (first order
in v/c)" (p. 498).
"One
of the most debated problems in special relativity"! As is clear from
my last few posts, that's not exactly reflected in some recent textbooks
on special relativity purportedly focusing on conceptual issues.
Mansouri
and Sexl quickly make it clear that they believe convention plays an
important role in clock synchronization and thus in the definition of
simultaneity. They state, for example, that "Einstein's procedure to
synchronize clocks at different space points is but one of several
possible alternative conventions".
Mansouri
and Sexl are thus effectively saying that the synchronization of clocks
is a matter of convention. They do not give any particular reason for
this statement beyond listing a number of clock adjustment procedures
which they all label synchronization procedures.
And
that's the crux of the matter. I think it's important to be absolutely
clear about what exactly is conventional in Einstein's theory: it's the
choice of clock adjustment procedure. Anybody is free to adjust distant
clocks any way they like, and some such procedure may be adopted by a
whole community or even the whole world as the one to be applied by
convention. But, and this is a big but, not every clock adjustment
procedure is a synchronization procedure.
To
prove that point, it is sufficient to give examples of clock adjustment
procedures which are not synchronization procedures, and I have done
this in, for example, this and this
post. Drawing on those examples, I have argued that in general terms an
Einstein-like clock adjustment procedure using signals is a
synchronization procedure if and only if the signals used are emitted
and propagate in symmetrical conditions in all directions. And I have
concluded that on that basis Einstein's clock adjustment procedure is
not and cannot be a synchronization procedure.in all uniformly moving
frames of reference.
All
that may seem straightforward enough. But there is a possible objection
to my line of reasoning which I think I need to address in greater
detail than I have done.
The
objection broadly goes like this: "True, there may have been a time
when the idea of simultaneity was based on that of sending out signals
in symmetrical conditions, but that concept of simultaneity has become
untenable because it's emerged that it's impossible to distinguish
between frames of reference in which such symmetry pertains and frames
in which it doesn't. Therefore physicists have redefined
the concept and have agreed to call distant events with the same time
stamp according to Einstein-adjusted clocks "simultaneous". Even if that
definition hasn't filtered through into general usage, it's a technical
definition of the kind scientists use all the time to ensure their
concepts are precise and can be applied operationally. For example,
mathematicians talk about "groups" and "rings" in algebra in a very
precise technical sense, and they're perfectly free to do so even though
the concepts of a "group" or "ring" are used in very different ways in
non-mathematical contexts."
Indeed.
Absolutely. Physicists are free to do this. But then they shouldn't be
using the concept of "simultaneity (physics)" in contexts in which only
the symmetry-based concept of simultaneity makes sense. Just like
mathematicians shouldn't - and to the best of my knowledge generally
don't - use their concept of a "group (algebra)" to talk about group
dynamics in social situations, for example.
To
be more specific: I think the concept of simultaneity is closely linked
to concepts such as synchronization, symmetry, existence, signal,
speed, and cause and effect. This link is established in the way people
generally think, talk and write about these various concepts. It is thus
ingrained in the English language as currently constituted. Similar
considerations probably apply to many other languages in which similar
concepts exist.
I think the following statements exemplify some of the relationships between those concepts as currently constituted:
1)
Events in two places A and B are simultaneous if and only if
synchronized clocks located at A and B show the same time when the
events occur.
2)
Clocks in A and B can be synchronized by setting them to the same time
when identical signals emitted in opposite directions from the mid-point
M between A and B arrive at the clocks, provided the signals propagate
in symmetrical conditions.
3)
Signals sent from A to B cannot arrive in B at an earlier time than
when they were emitted as measured by synchronized clocks in A and B.
4)
If a signal emitted from A arrives in B at an earlier time than when it
was emitted, according to clocks positioned in A and B, then those
clocks aren't synchronized.
5)
A cause in a location A always precedes its effect at a distant
location B provided the clocks used to measure time in A and B are
synchronized.
6)
The one-way speed of a signal between A and B is the distance between A
and B divided by the time the signal needs to travel from A to B as
measured by synchronized clocks in A and B.
Some
of the meaning of "simultaneity", "synchronization", "symmetry",
"signal", "speed" and "cause and effect" is established in these
relationships.
It
is thus not possible to "redefine" one such concept and expect its
relationship with other, related concepts to be unaffected. For example,
I would hold that the concept of cause and effect relies on a
symmetry-based concept of simultaneity and becomes inapplicable in some
circumstances if the requirement of symmetry is given up.
And
this is exactly what happens if Einstein's clock adjustment procedure
is adopted: while we may not know whether light signals propagate
symmetrically in any particular uniformly moving frame of reference, we
do know that if they propagate symmetrically in a first frame then they
do not propagate symmetrically in other frames that move relative to the
first, at least not locally. The result is that the concept of cause
and effect, for example, becomes inapplicable in the context of special
relativity if superluminal speeds are involved.
Suggestions that superluminal speeds lead to cause and effect or the flow of time being "reversed", as they keep being made
in relation to recent neutrino experiments at CERN, are thus misguided:
they are the result of uncritically and unwittingly applying concepts
that rely on a symmetry-based concept of simultaneity to a theory in
which that concept has been abandoned.
After
this little digression, it's time to mention the second statement made
by Mansouri and Sexl that is pertinent to my investigations. This is the
"remarkable result", as the authors describe it, that "a theory maintaining absolute simultaneity is equivalent to special relativity" (Mansouri/Sexl's emphasis, p. 503).
My discussion of this statement will, however, have to wait until my next post.
Vesselin Petkov's Relativity and the Nature of Spacetime (2005) promises to specifically address "conceptual questions" relating to special relativity, such as "the physical meaning of the relativity of simultaneity" (p. 1, Petkov's emphasis), so this book should be right up my street.
As it turns out, it is anything but. The reason is that, far from probing the foundations of special relativity, Petkov takes them for granted. What is more, he takes a literal interpretation of those foundations for granted, no questions asked.
More specifically, of the three questions I have raised in previous posts:
- how decision-making contributes to the principle of the constancy of the speed of light;
- why it may be useful or advisable to adjust clocks in line with Einstein's procedure;
- and whether or in what sense Einstein's clock adjustment procedure can be regarded as a synchronization procedure and whether, therefore, it leads to meaningful statements about one-way speeds, simultaneous existence and causality
Petkov answers none. In fact, he doesn't even mention Einstein's clock adjustment procedure or the issue of clock synchronization, so in that sense he has even less to say about these issues than Leo Sartori in Understanding Relativity (1996), if that's possible.
How then does Petkov explain the principle of the constancy of the speed of light? He says it's a consequence of Galileo's principle of relativity, which according to him states that "by performing mechanical experiments, the uniform motion of a body cannot be detected" (p. 26). Petkov later makes it clear that by "motion" he means "absolute motion" relative to "some kind of medium" that pervades all of space (pp. 30-32).
Petkov seems to take the empirical finding that the two-way speed of light is always c for granted since he moves straight to the issue of the one-way speed of light. He argues that observers who "determine" or "see" or "observe" that the speed of light is not the same in every direction "would discover their absolute uniform motion", and since that's not possible according to the relativity principle they cannot observe any such thing (pp. 40-41).
What Petkov fails to realize, or to mention, is that in the first instance the constancy of the speed of light in every direction is not a matter that can be "determined" or "seen" or "observed" because before we can make such an observation we first need to adjust distant clocks. To do that, we need to decide on a clock adjustment procedure. We could, for example, try to adjust our clocks such that those clocks are synchronized, in other words such that equal time coordinates define a relationship of simultaneity.
As Einstein observed, two clocks may be synchronized by setting them to zero when a signal sent in all directions from the mid-point between the two clocks arrives there - provided the conditions of signal emission and propagation are symmetrical in all directions. Concepts such as one-way speed, simultaneous existence and causality are interwoven with and depend on this notion of simultaneity.
But, as Max Born suggested, it is difficult to be sure whether the conditions in which light or anything else propagates are symmetrical in every direction because we don't know the full list of parameters on which such symmetry might depend. I have proposed that local acceleration history might be one such parameter that is missing from current models, but this is just an idea at this stage, an idea which I will have to explore in much greater detail in the months and years to come.
Einstein adopted a different approach: he effectively proposed that we should dispense with the requirement of synchronization and instead adjust our clocks such that the laws of physics, in particular those of electrodynamics, take on a particularly simple form. Out of that, the elegant theory of special relativity was born. Elegant certainly, but with the drawback that the concepts of one-way speed, simultaneous existence and causality are no longer fully applicable in that theory.
There is thus more to special relativity than Petkov's formulation of Galileo's principle of relativity. In particular, special relativity is partly based on Einstein's choice of clock adjustment procedure with all its conceptual consequences. This issue is completely lost to Petkov. Instead, he takes Einstein's clock adjustment procedure and the idea that it represents a synchronization procedure for granted. Literally. For he concludes that according to relativity every event is simultaneous with every other in this world and that we therefore live in a block universe in which the flow of time is just an illusion - a typical example of the simultaneity syndrome in modern physics.
Over my last few blog entries, I have looked at the way in which three contemporary specialists on special relativity discuss the role of decision-making or convention in the principle of the constancy of c, in textbooks or monographs that set out to clarify the main conceptual issues relating to special relativity. What I have found is that neither Sartori (1996) nor Rindler (2001) nor Petkov (2005) even mention, let alone discuss, the issue of whether or in what sense Einstein's clock adjustment procedure is a synchronization procedure, and only Rindler suggests an answer to the question of why it may be useful or advisable to adopt Einstein's procedure.
I think the time has now come for me to turn my attention to some other texts in the literature which I hope and believe offer deeper answers to my questions. The first of these is an article published in 1977 by Reza Mansouri and Roman U. Sexl, followed finally by Kevin Brown's very important book, Reflections on Relativity (2010).
